Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Provas antigas – Cálculo 2 – Unicamp – P2 5ª tarde – questão 1
Calcule a integral:
Dica: inverta a ordem de integração
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
Poderíamos tentar de n maneiras resolver a integral na ordem em que está, mas isso resultaria muito trabalho e as vezes não funciona.
Sendo, assim... lembrando que é uma prova, queremos poupar tempo, e ganhar nossos pontos fazendo tudo estando convictos dos pontos. Assim, vamos inverter a ordem de integração, ou seja, substituir dydx por dxdy
Mas é tão fácil assim? Não, não é. Lembre-se que o intervalo de 0 a 1 é para o dx, e não para o dy, e ele é satisfeito se dy vem antes, pois veja que dy tem intervalo que depende x.
Bom, então temos que olhar novamente para os limites e reanalisar quais que devem ser os novos limites.
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Sendo assim, façamos o esboço do gráfico dos intervalos de integração de x e y:
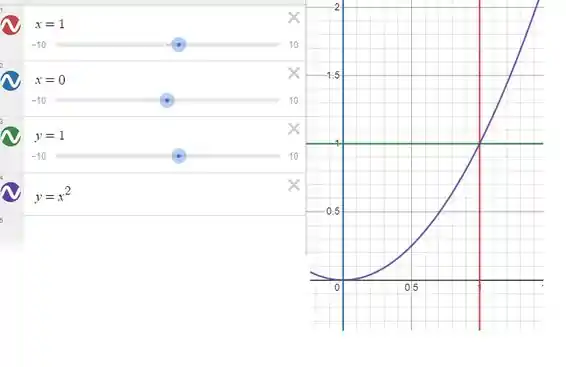
Onde estão as curvas e suas cores nas legendas.
Veja carinha, que se queremos trocar de dydx para dxdy, concorda comigo que devemos analisar primeiro dx? Porque é com ele que vamos começar a integração.
Assim, vemos que com relação ao eixo y, x percorre de 0 e segue a função , e y nesse caminho percorre de 0 até 1, resumindo:
De forma que a nossa integral fica:
E vai ver que agora a vida é um morango hashushua, essa integral vai sair mole mole.
Passo 3
Integrando em x:
Veja que temos dois termos com e para facilitar ainda mais, façamos uma susbtistituição:
De forma que:
E quando fazemos uma substituição, qualquer que seja, devemos fazer uma analise de como que os novos limites d integração reagem à essa nova interação, sendo assim:
Assim a nossa nova integral fica:;
E agora basta integrarmos o seno.
Sabemos que a integral do seno é menos o cosseno. Logo:
E assim achamos o resultado da nossa integral.
Resumindo: