Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
- Calcule as seguintes integrais:
Passo 1
Bem...! Em exercícios como esse, você tem que ficar muuuuito atento, pois embora a integral talvez até dê para resolver, você perderia muito tempo de prova! Por isso pare, pense e reflita antes de qualquer conta, ok?
Nesse exercício vamos, portanto, realizar uma troca da ordem de integração e ver se isso nos ajuda, bora?
Passo 2
Para trocar a ordem como planejamos, devemos antes desenhar a região de integração, mas não se preocupe, pois isso pode ser feito retirando algumas informações da própria integral:
- como o está mais externo, os limites mais externos são dele, portanto:
- Enquanto isso:
Com esses dois intervalos retirados da integral, você sempre ganha equações:
E advinha? Sim, vamos desenhar essas curvas no plano !
Passo 3
Comecemos com as três primeiras mais simples equações:
e , ambas duas retas bem simples paralelas ao eixo (inclusive é o próprio eixo )
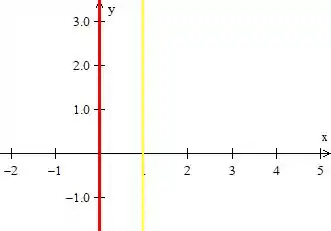
também é uma reta bem simples, porém dessa vez ela é paralela ao eixo . Veja!
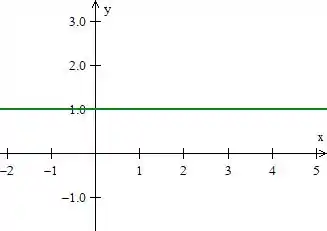
Um pouquinho mais “elegante” que essas está a curva da raiz de ()
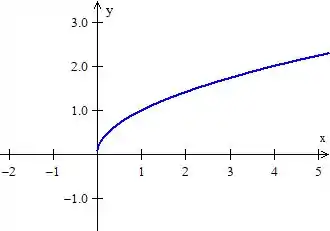
Juntando as três curvas, logo podemos perceber a região que estamos trabalhando entre as ;)
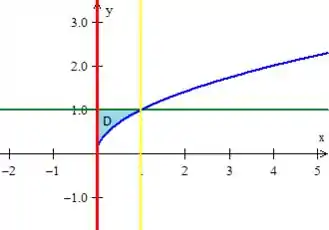
Passo 4
O que devemos fazer agora é trocar a ordem de integração!
Pow! Se antes estávamos trabalhando com variando em um intervalo numérico, isso implicava que estávamos trabalhando com a região configurada do . Então, a gente vai configura-la agora do Tipo 2 :D!
Nessa configuração, temos o que varia entre dois números reais, no caso ele varia de até a reta verde;
Não podemos nos esquecer da variação do também!
entra na reta vermelha e sai na curva azul (acompanhe a reta PRETA com o seu dedo e veja )
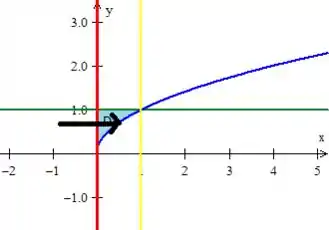
Logo
Como a curva azul é , isolando o ...
Onde concluímos que
Passo 5
Basta agora colocar essa nova variação
dentro da integral dupla (mas não se esqueça que o limite numérico sempre vem primeiro )...
Repare que agora a inversão está concluída e podemos prosseguir com a resolução da integral. Bora?
Passo 6
Calculando primeiro a integral de dentro...
Como a função de dentro depende apenas de e estamos integrando em podemos a considerar como uma constante fazendo-a vazar de dentro dessa integral...
Substituindo os limites de integração em ...
Tchaaaaram!!! Eis o motivo disso tudo! Essa integral é moleza, basta que façamos uma mudança de variável ;)
Não se esqueça de trocar os limites também, heim!
Finalmente, substituindo tudo...
substituindo os limites...