Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
PUCRIO – Cálculo 3 – MAT1163 – 2020.2 – G3 – Discurciva
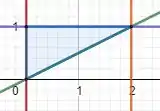
Considere a integral iterada
Esboce a região de integração.
Inverta a ordem de integração.
Calcule a integral.
Passo 1
Vem comigo que a gente detona com essa questão juntos!
Temos uma integral dupla em mãos.
E nós temos que esboçar a região onde ela está sendo calcula, ou seja, temos que desenhar a região onde acontece a integração e a gente usa os limites de integração como base para isso.
O item pede para invertermos a ordem de integração, ou seja, em vez de calcular na ordem , vamos calcular na ordem , mas não é só trocar as integrais de lugar, os limites de integração mudam por conta disso.
E por último no item temos que resolver essa linda integral.
Vamos nessa então!
Passo 2
Vamos começar esboçando a região pedida em .
Essa região na direção varia de até e na direção varia de até , então ela fica da seguinte forma:
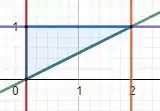
A região é essa que está em azul.
Passo 3
Agora vamos inverter a ordem de integração que o item pede.
Temos que colocar nossa integral em , então vamos primeiro ver os limites de integram em .
O olhando a região que desenhamos em , dá para ver que os valores de partem do zero, até encostar na reta azul, essa reta azul é definida por:
Invertendo essa função temos:
Então varia de à . Agora vamos ver o limite de integração em , olhando a região novamente, a gente consegue ver que varia de até .
Usando isso então a integral fica da seguinte forma:
Passo 4
Agora vamos integrar a integral que reescrevemos em , temos:
Como estamos integrando primeiro em e a função não depende de , temos:
Passo 5
Agora para resolver essa integral em , vamos usar a técnica de substituição, vamos chamar
E os limites de integração ficam da seguinte forma:
E
A integral fica seguinte forma:
Então temos que:
Resposta
