Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Dada a integral iterada
(a) Esboce a região de integração
(b) Inverta a ordem de integração
(c) Calcule a integral
Passo 1
Letra (a)
Fala galera, vamos pegar as informações que precisamos dessa integral pra responder essa primeira letra aí!
Pra fazer um esboço da região, precisamos dos limites dados na integral, nesse caso a integral de dentro está associada a , certo? Então ela nos dá os limites de .
Os limites da integral de fora, por consequência, estão associados a , portanto
Sabendo disso, a região é essa aqui
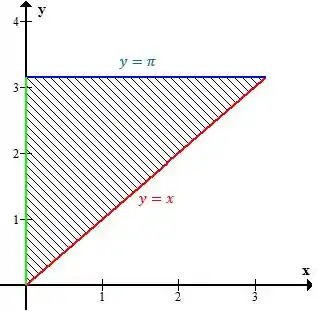
Passo 2
Letra (b)
Vamos agora pensar em como inverter essa região. Ela ta escrito primeiramente como em função de , certo? Então isso é uma região do tipo .
Precisamos pegar esses limites e colocar em função de ! Mais do que isso, precisamos ver os limites de integração da esquerda para a direita, não mais de baixo pra cima, olha só
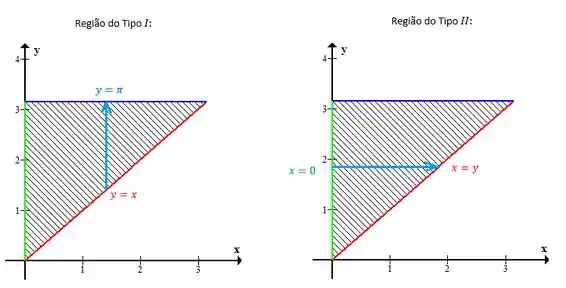
Portanto é limitado inferiormente por e superiormente por , portanto
Agora é só olhar os limites numéricos de . Da pra ver que começa em e vai até a reta azul que é , portanto
Com isso a nova integral fica
Passo 3
Letra (c)
Para calcular a integral, vamos usar a integral invertida, por que isso?
Tentar integrar primeiro em pode até ser possível, mas parece bem difícil! Vamos ver que fazendo em primeiro vai facilitar bastante as coisas, vamos lá?
Passo 4
Integrando isso aí em relação a , perceba que tudo ali dentro só tem , certo? Então a integral em fica
Integrando em relação a