Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Origem do Exercício
Resolva a integral:
Invertendo a orgem de integração.
Passo 1
Para inverter a ordem de integração, é essencial fazer um esboço da região!
Então vamos lá, nossa situação é a seguinte, o varia nesse intervalo:
E para cada nesse intervalo, o varia entre uma função e uma constante:
Então estamos integrando nessa região aqui:
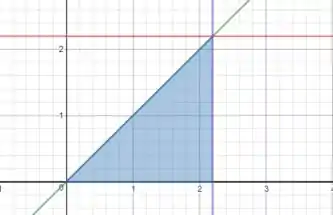
Passo 2
Então tá, antes tínhamos fixado a variação do com constantes. Para trocar a ordem de integração, vamos fixar o com constantes!
Olhando para a região, quais limites podemos colocar para o ?
Agora vamos escolher um ponto qualquer do eixo , qual o intervalo em que ele varia no eixo ?
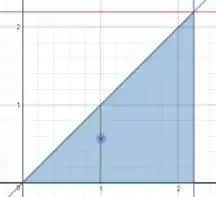
A coordenada daquele ponto roxo ali, por exemplo, vai variar nesse intervalo:
Esse no limite superior vem do fato de que aquela reta na diagonal é a função .
Passo 3
Então beleza, agora já temos os intervalos que as duas variáveis percorrem:
Substituindo isso na integral (que vamos chamar de ):
Agora sim, essa é uma integral que podemos resolver.
Passo 4
Primeiro vamos integrar em relação a , nesse caso lembre que vamos tratar o como uma constante, então o pode simplesmente ser colocado pra fora da integral!
E o valor da integral é:
Colocando isso de volta na integral dupla:
Passo 5
Aqui podemos fazer uma substituição simples:
E os limites de integração também precisam ser trocados:
Agora vamos substituir tudo isso na integral:
E como a integral de é simplesmente :
Pronto, resolvemos a integral!
Resposta
O valor da integral é .