Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
UFJF. Cálculo 3. Lista de Estudos. Lista da AV1 – 2022.2. Questão 2.
2. Dê a inversão da ordem de integração de .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão foi dada uma integral e o que temos que fazer é inverter a ordem de integração de para .
Como fazemos isso? 👀
Podemos pensar que seria só trocar e de lugar, trocando também os limites de integração ficando como
Mas não é tão simples assim, perceba que se fizermos isso, na última integral vamos obter alguma coisa em função de e não queremos isso.
Então como fazemos isso?
Bora ver! 😁
Passo 2
Primeiramente, vamos analisar os limites de integração da integral.
Se a integral é dada por
Vemos que em os limites variam entre e . Isso significa que os limites de integração em é dado pelas equações e
Com essas equações obtidas, vamos inverter a jogada e isolar em um lado da igualdade.
Para a equação , temos
Elevando os dois lados ao quadrado
Agora para a equação , temos
Tirando a raiz cúbica de cada lado...
Entendeu essa parte? 🤩
Passo 3
Agora, vemos que em os limites de integração variam entre e , ou seja, e .
Substituindo por nas equações que acabamos de obter, temos
Fazendo a substituição de por ...
Para a outra equação, temos
Elevando os dois lados ao cubo...
Substituindo por
Com isso, vemos que o limite superior que na configuração inicial era de , agora é de .
Agora para obter o limite inferior, substituímos por .
Na primeira equação, temos
Na segunda equação
Assim, vemos que o limite inferior em será .
Está acompanhando? 😎
Passo 4
Por fim, vamos juntar as informações que obtemos e montar nossa nova integral.
Os limites de integração em é dado pelas equações e .
Já em , os novos limites de integração são dados por e .
Esboçando a região limitada por essas curvas, temos
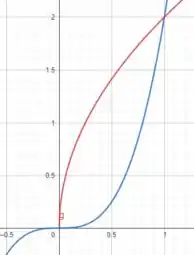
Onde a curva azul é dada por e a vermelha por .
Assim vemos que o limite superior em é dado por e o limite inferior por .
E finalmente, montando nossa integral, vamos obter
Entendeu tudo? 😉
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
