Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 3b.
3 - Inverta a ordem de integração das seguintes integrais duplas iteradas:
b)
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Essa questão parece ser rapidinha, não é? Saiba que você está correto!
O que temos que fazer é inverter os limites de integração de uma função qualquer dada por
Mas aí a gente imagina que seja simplesmente mudar as integrais de lugar, não é?
Calma lá, essa questão é rápida, mas nem tanto!
Perceba que no fim dessa integral, quando aplicarmos os limites de integração, vamos obter um número. Já se simplesmente trocarmos as integrais de lugar no fim, vamos aplicar a variável nos limites de integração, o que var nos resultar em uma função.
A gente faz essa mudança de quando temos uma integral muito difícil de início e invertendo os limites de integração vamos obter o mesmo resultado, mas de uma forma muito mais fácil.
Veja só como fazemos essa mudança.
Passo 2
Primeiro de tudo, vamos desenhar nossa região de integração.
Perceba que para , os limites de integração vão de a . Já para , os limites vão de a .
Com isso, temos quatro curvas que limitam nossa integral.
Vamos plotar essas curvas pra visualizar a região
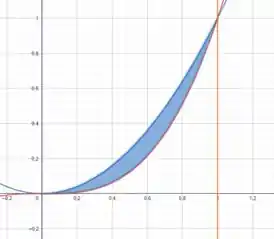
Essa é nossa região de integração.
O que temos que fazer agora é encontrar uma maneira de escrever os intervalos de entre dois valores e de entre as duas funções.
E como fazemos isso? 🤔🤔
Passo 3
Normalmente, o limite superior da integral é composto pela maior curva, isso para evitar resultados negativos.
Vamos olhar para o eixo primeiro, no gráfico da região podemos ver que está hachurado no intervalo de a .
Podemos provar isso substituindo os limites superiores e inferiores anteriores, tínhamos
Substituindo nas equações vamos encontrar
Logo, esse é o nosso intervalo para .
Agora com relação ao eixo , vemos que a região está variando entre as duas curvas.
Temos a relação entre e dessas curvas.
Se manipularmos essas equações para isolar em um lado da equação, vamos obter
Como os limites de integração vai da maior curva para a menor, temos que varia de a . Logo esse é nosso intervalo em .
Com isso, nossa integral será
Fim! Iae, o que achou? Responde Aí! 😁
