Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas

Ver Teoria
Exercício 75123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737476777879808182838485868788899091929394

Enunciado

Integrais Duplas sobre regiões gerais

Considere a função g : 1,4 → R definida por

g x = x , 1 ≤ x ≤ 2 2 , 2 ≤ x ≤ 4

E a região plana

R = x , y ∈ R 2 x ≤ y ≤ g x ,   1 ≤ x ≤ 4

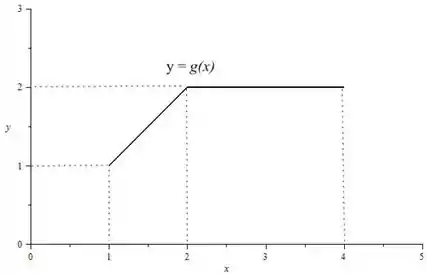
  1. Esboce o gráfico da função g
  2. Esboce a fronteira de R e ao lado esboce o interior de R
  3. Descreva a região plana R na forma

    4. R = x , y ∈ R 2 f 1 y ≤ x ≤ f 2 y ,   a ≤ y ≤ b

  4. Calcule a integral dupla

I = ∬ R sen ⁡ π x 2 y d x d y

Usando o método que preferir.

Passo 1

a )

A função g vai ser uma reta inclinada entre x = 1 e x = 2 e depois vai ficar horizontal, olha como é o seu gráfico

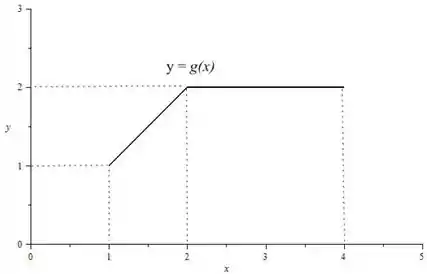
Passo 2

b )

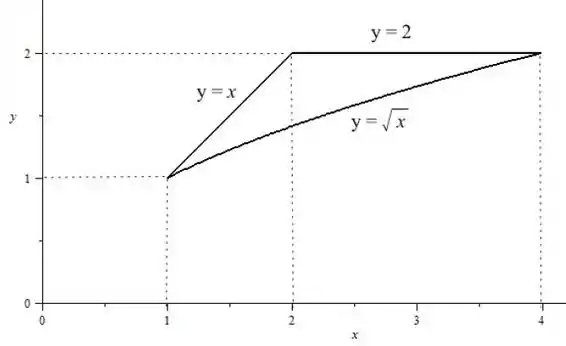
Temos que fazer a região R , repara que uma parte dela já fizemos, que é g x . Vamos ver em que pontos as duas funções se cortam, para entendermos como fica essa região R .

Começando com a parte de g x onde 1 ≤ x ≤ 2

x = x

x = x 2

x 2 - x = 0

x x - 1 = 0

x = 0

Ou

x = 1

Como essa parte da função está limitada à 1 ≤ x ≤ 2 eles vai se encontrar em x = 1

Vamos ver agora a parte onde 2 ≤ x ≤ 4

x = 2

x = 2 2

x = 4

Beleza então as funções se cruzam nos limites de R . O gráfico vai ficar

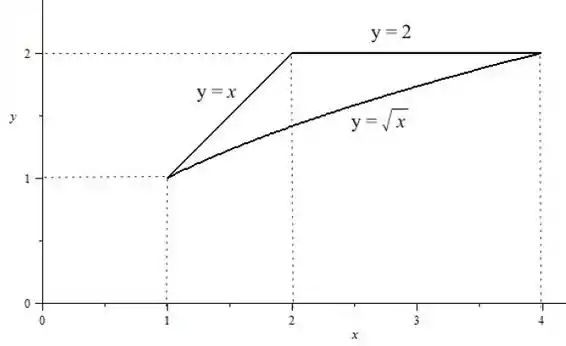
Não pintamos a parte de dentro porque ele quer a fronteira, ou seja, só esse limite.

Passo 3

c )

Aqui vamos precisar reescrever a região como uma região do tipo II.

Pelo gráfico conseguimos ver que y vai de 1 à 2 . Isso nos diz que

1 ≤ y ≤ 2

A os valores de x vao de x = y até y = x . Essa última função é a mesma coisa que y 2 = x , então vamos ter

y ≤ x ≤ y 2

R = x , y ∈ R 2 y ≤ x ≤ y 2 , 1 ≤ y ≤ 2

Passo 4

d )

Vamos agora fazer a integral

I = ∬ R sen ⁡ π x 2 y d x d y

Vamos usar R como uma região do tipo II porque já temos o intervalo assim e ele não é nada bizarro, a integral vai ficar

I = ∫ 1 2 ∫ y y 2 sen ⁡ π x 2 y d x d y = ∫ 1 2 - cos ⁡ π x 2 y π 2 y x = y x = y 2 d y = ∫ 1 2 - 2 y π cos ⁡ π x 2 y x = y x = y 2 d y

⇒ ∫ 1 2 - 2 y π cos ⁡ π y 2 2 y - - 2 y π cos ⁡ π y 2 y d y = ∫ 1 2 - 2 y π cos ⁡ π y 2 + 2 y π cos ⁡ π 2 d y

⇒ ∫ 1 2 - 2 y π cos ⁡ π y 2 d y = - 2 π ∫ 1 2 y cos ⁡ π y 2 d y

Vamos resolver essa integral

Passo 5

∫ y cos ⁡ π y 2 d y

Vamos usar a integração por partes

u = y

d v = cos ⁡ π y 2 d y

Isso nos diz que

d u = d y

v = sen ⁡ π y 2 π 2 = 2 π sen ⁡ π y 2

Lembrando que a integração por partes é

∫ u d v = u v - ∫ v d u

Então

∫ y cos ⁡ π y 2 d y = 2 π y sen ⁡ π y 2 - ∫ 2 π sen ⁡ π y 2 d y = 2 π y sen ⁡ π y 2 - 2 π ∫ sen ⁡ π y 2 d y

⇒ 2 π y sen ⁡ π y 2 - 2 π ∫ sen ⁡ π y 2 d y = 2 π y sen ⁡ π y 2 - 2 π - cos ⁡ π y 2 π 2

⇒ 2 π y sen ⁡ π y 2 + 4 π 2 cos ⁡ π y 2

Passo 6

Voltando para a integral lá de cima

- 2 π ∫ 1 2 y cos ⁡ π y 2 d y = - 2 π 2 π y sen ⁡ π y 2 + 4 π 2 cos ⁡ π y 2 y = 1 2

⇒ - 2 π 2 π 2 sen ⁡ π 2 2 + 4 π 2 cos ⁡ π 2 2 - 2 π 1 sen ⁡ π 1 2 + 4 π 2 cos ⁡ π 1 2

⇒ - 2 π 4 π sen ⁡ π + 4 π 2 cos ⁡ π - 2 π sen ⁡ π 2 + 4 π 2 cos ⁡ π 2

⇒ - 2 π - 4 π 2 - 2 π

I = - 2 π - 4 π 2 - 2 π = 8 π 3 + 4 π 2

Resposta

  3. R = x , y ∈ R 2 y ≤ x ≤ y 2 , 1 ≤ y ≤ 2
  4. I = 8 π 3 + 4 π 2

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos ⁡ x1 + cos 2 ⁡ xd xd y
Inverta a ordem de integração.