Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas

Ver Teoria
Exercício 54123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525355565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

Integrais duplas sobre regiões gerais

Calcule a integral

∫ 0 π ∫ 0 y cos ⁡ ( x / π )   y - x x - π 2 d x d y

Esboce a região de integração.

Passo 1

Vamos começar fazendo o esboço dessa região. Temos x variando desde x = 0 até a reta x = y e y variando desde y = 0 até y = π , portanto:

0 ≤ x ≤ y

0 ≤ y ≤ π

Isso nos dá a seguinte região:

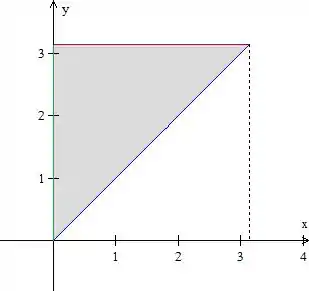
Repare que x está entre a reta verde e a azul, enquando y varia entre números, portanto, a região fois escrita como do tipo II.

Passo 2

Analisando a questão, percebemos que temos um problema, não sabemos integrar cos ⁡ ( x / π )   y - x x - π 2 em relação a x . Então, usaremos um artifício para fugir dessa integral, inverter a ordem de integração. Precisamos, então, reescrever a região acima como tipo I.

Pelo gráfico, vemos que x varia entre 0 e π e que y varia entre as retas y = x e y = π . Pronto, basta levar esses valores para a integral de forma invertida, teremos:

∫ 0 π   ∫ x π cos ⁡ ( x / π )   y - x x - π 2 d y d x

Você verá que essa troca facilitará muito nossa vida!

Passo 3

Vamos integrar, então, em relação a y :

= ∫ 0 π   ∫ x π cos ⁡ x π x - π 2 ( y - x ) d y d x

= ∫ 0 π   cos ⁡ x π x - π 2 y 2 2 - x y x π d x =

= ∫ 0 π   cos ⁡ x π x - π 2 π 2 2 - π x - x 2 2 - x 2 d x =

= ∫ 0 π   cos ⁡ x π x - π 2 π 2 2 - π x - - x 2 2 d x =

= ∫ 0 π   cos ⁡ x π x - π 2 π 2 2 - π x + x 2 2 d x =

Podemos colocar 1 / 2 em evidência, ficando

= 1 2 ∫ 0 π   cos ⁡ x π x - π 2 π 2 - 2 π x + x 2 d x

Repara que

π 2 - 2 π x + x 2 = π - x 2

Então, a nossa integral vai ficar

= 1 2 ∫ 0 π   cos ⁡ x π x - π 2 π - x 2 d x =

= 1 2 ∫ 0 π cos ⁡ x π d x =

= 1 2 ∫ 0 π cos ⁡ x π d x

Passo 4

Agora, vamos integrar em relação a x :

= π 2 s e n x π 0 π =

= π 2 s e n ( 1 )

Resposta

π 2 s e n ( 1 )

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos ⁡ x1 + cos 2 ⁡ xd xd y
Inverta a ordem de integração.