Calcule as seguintes integrais:
Passo 1
Eita, a primeira vista essa integral parece impossível de calcular, né?
Mas calma que pra tudo nessa vida tem jeito! Nesse caso, vamos inverter a ordem de integração pra ver se melhora.
Primeiro de tudo, vamos fazer o esboço do domínio. Temos uma região do tipo , com , o limite de inferior de x é uma constante, , mas o superior é uma função de , .
No desenho, a região fica assim:
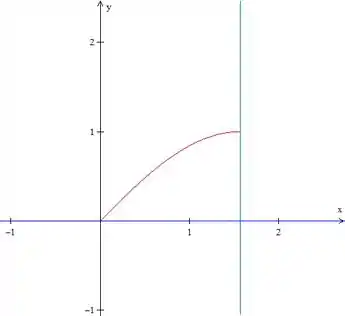
Que não é muito difícil de se escrever como tipo , vamos ver como vai ficar.
Passo 2
Os limites de são bem claros, e os de também não são nada muito difícil de ver, . Então nossa integral vai ficar:
Passo 3
Resolvendo a integral, a gente vai chegar em:
Que a gente resolve pela substituição:
Então:
Aplicando os limites de integração:
Viu, nada tão complicado assim, né?