Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 3a.
3 - Inverta a ordem de integração das seguintes integrais duplas iteradas:
a)
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Essa questão é bem rapidinha, veja só
Temos uma integral de uma função qualquer dada por
Podemos usar este método quando temos uma integral muito complicada de inicio com a primeira integral. Então trocamos a ordem de integração para facilitar nossos cálculos.
Aí podemos pensar: “é fácil, só trocar as integrais de lugares”. Mas é aí que a gente se engana.
Perceba que temos que fazer a troca, mas não podemos mudar o resultado, se fizermos isso, no final vamos ter uma variável depois da substituição dos limites de integração.
Ou seja, é simples, mas não quanto parece! Bora lá!
Passo 2
A primeira coisa a se fazer é desenhar a região de integração pra facilitar nos passos seguintes.
Perceba que para a integral com relação a , os limites de integração vão de a 0, já para , os limites de integração vão de a .
Com isso, vamos ter quatro curvas que limitam nossa região
Se plotarmos essas curvas e hachurar a área em comum dessas variâncias para e .
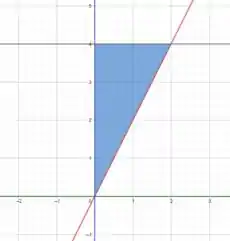
Agora, o que precisamos fazer é descrever a variação de por meio de duas constantes e por meio de uma ou duas funções.
Vish, como podemos fazer isso?
Passo 3
Podemos observar que está variando entre e . Ou podemos mostrar que se , na extremidade , temos
Com isso, já obtemos os limites de integração para .
Com relação a , temos a função
Isolando de um lado, temos
Esse é um dos limites de integração.
Sempre dizemos que os limites de integração variam da maior curva para a menor curva. Ou seja, para , a região de integração está descrita de até a curva que acabamos de obter, .
Ou seja, os limites de integração para , é de a .
Montando nossa integral, vamos ter
Para visualizar de forma mais clara essas informações é muito necessário ter prática, então bora praticar mais!
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
