Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas

Ver Teoria
Exercício 26123456789101112131415161718192021222324252728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

UFSCAR. Cálculo 3. Lista de Estudos – Integrais Duplas. Questão 9.

9 – Considere ∫ 0 2 ∫ - y y ( x y 2 + x ) d x d y . Reescreva esta mesma integral invertendo a ordem de integração. Como ficariam os limites de integração agora? Qual o valor desta integral?

Passo 1

Fala aí. Tudo belezinha com você? Vem comigo resolver mais uma questão de integrais duplas.

E pra começar, vamos entender esse enunciado aí. Veja bem, a questão pede pra gente reescrever esta integral

∫ 0 2 ∫ - y y ( x y 2 + x ) d x d y

Invertendo a ordem de integração.

Mas calma aí, porque aqui não podemos simplesmente trocar o d x d y por d y d x , isso faria com que nós estivéssemos integrando uma região totalmente diferente. Então para garantir que vamos fazer a trocar e manter a região de integração igual, nós precisaremos corrigir também os limites de integração. Belezinha???

E para fazer isso, vamos desenhar a região de integração para ver como fazer essa troca e depois calcular de fato a integral.

Vamos ver como fica no nosso caso? 😎

Passo 2

A integral original é

∫ 0 2 ∫ - y y ( x y 2 + x ) d x d y

E podemos ver que x está variando entre as funções

- y ≤ x ≤ y

E y está variando entre as constantes

0 ≤ y ≤ 2

Então, desenhando essa região encontraremos:

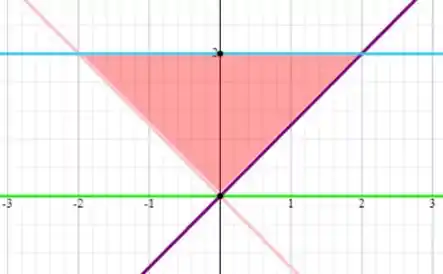
Para inverter a ordem de integração precisaremos com que a integral fique desse jeito aqui:

∫ x 1 x 2 ∫ f 1 ( x ) f 2 ( x ) ( x y 2 + x ) d y d x

Ou seja, y precisa variar entre funções e x entre constantes. Mas um detalhe importante que precisaremos ter cuidado é que a variação de y não é a mesma em toda a região. Então precisaremos dividir essa região em duas partes.

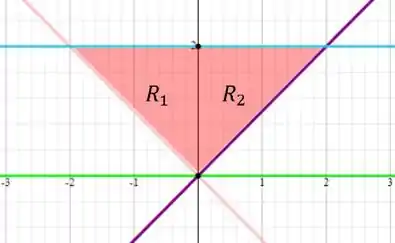
Para a região R 1 o y está variando entre as funções f x = - x e g x = 2

Assim:

- x ≤ y ≤ 2

E os valores de x estão variando entre as constantes - 2 e 0 .

- 2 ≤ x ≤ 0

E para a região R 2 o y está variando entre as funções f x = x e g x = 2

Assim:

x ≤ y ≤ 2

E os valores de x estão variando entre as constantes 0 e 2 .

0 ≤ x ≤ 2

Agora que já temos os novos limites de integração, só nos resta resolver a integral, sendo:

∫ 0 2 ∫ - y y ( x y 2 + x ) d x d y = ∫ - 2 0 ∫ - x 2 ( x y 2 + x ) d y d x + ∫ 0 2 ∫ x 2 ( x y 2 + x ) d y d x

Bora fazer isso no próximo passo.

Passo 3

Resolvendo a integra utilizando o Teorema de Fubini, teremos:

∫ - 2 0 ∫ - x 2 x y 2 + x d y d x + ∫ 0 2 ∫ x 2 x y 2 + x d y d x

∫ - 2 0 ∫ - x 2 x y 2 + x d y d x + ∫ 0 2 ∫ x 2 x y 2 + x d y d x

Resolvendo a integral de dentro

∫ - 2 0 x y 3 3 + x y | - x - 2 d x + ∫ 0 2 x y 3 3 + x y | x 2 d x

Aplicando os limites de integração

∫ - 2 0 x ⋅ 2 3 3 + x ⋅ 2 - x - x 3 3 + x - x d x + ∫ 0 2 x ⋅ 2 3 3 + x ⋅ 2 - x ⋅ x 3 3 + x ⋅ x d x

∫ - 2 0 8 x 3 + 2 x - - x 4 3 - x 2 d x + ∫ 0 2 8 x 3 + 2 x - x 4 3 + x 2 d x

∫ - 2 0 8 x 3 + 2 x + x 4 3 + x 2 d x + ∫ 0 2 8 x 3 + 2 x - x 4 3 - x 2 d x

Show! Agora vamos resolver a integral de fora

4 x 2 3 + x 2 + x 5 5 + x 3 3 |   - 2 0 + 4 x 2 3 + x 2 - x 5 5 - x 3 3 |   0 2

Aplicando os limites de integração, ficaremos com:

0 - 4 ( - 2 ) 2 3 + ( - 2 ) 2 + ( - 2 ) 5 5 + ( - 2 ) 3 3 + 4 ⋅ 2 2 3 + 2 2 - 2 5 5 - 2 3 3 - 0

0 - 16 3 + 4 - 32 5 - 8 3 + 16 3 + 4 - 32 5 - 8 3 - 0

Ajustando os sinais, teremos:

- 16 3 - 4 + 32 5 + 8 3 + 16 3 + 4 - 32 5 - 8 3

Repara que todos as parcelas se cancelam.

Assim o resultado final da nossa integral é:

∫ 0 2 ∫ - y y ( x y 2 + x ) d x d y = ∫ - 2 0 ∫ - x 2 ( x y 2 + x ) d y d x + ∫ 0 2 ∫ x 2 ( x y 2 + x ) d y d x = 0

Resposta

∫ 0 2 ∫ - y y ( x y 2 + x ) d x d y = ∫ - 2 0 ∫ - x 2 ( x y 2 + x ) d y d x + ∫ 0 2 ∫ x 2 ( x y 2 + x ) d y d x = 0

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos ⁡ x1 + cos 2 ⁡ xd xd y
Inverta a ordem de integração.