Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas

Ver Teoria
Exercício 80123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798182838485868788899091929394

Enunciado

UFMG – Cálculo 3 – Lista 1 – Integrais duplas e triplas

1. Resolva as integrais duplas:

i) ∫ 0 1 ∫ arcsin ⁡ x π 2 e cos ⁡ y + 1 d y d x  

Passo 1

Falaaa... beleza???

Nessa questão vamos resolver a integral dupla.

Repara que se formos resolver nessa ordem vai ficar beeem difícil, então vamos usar a técnica de trocar a ordem de integração.

Passo 2

Primeiro precisamos desenhar a região de integração:

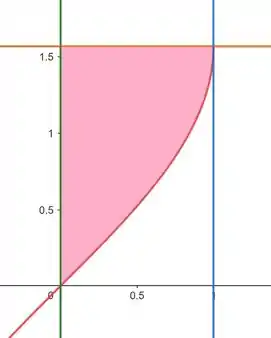
Repara que, se mudarmos a ordem, o y varia de 0 até π 2 e o x varia de 0 até sen ⁡ y .

A integral dupla fica:

∫ 0 π 2 ∫ 0 sen ⁡ y e cos ⁡ y + 1 d x d y  

Passo 3

Resolvendo a integral de dentro:

∫ 0 π 2 ∫ 0 sen ⁡ y e cos ⁡ y + 1 d x d y   = ∫ 0 π 2 x e cos ⁡ y + x 0 sen ⁡ y d y

= ∫ 0 π 2 sen ⁡ y e cos ⁡ y + sen ⁡ y d y

= ∫ 0 π 2 sen ⁡ y e cos ⁡ y d y + ∫ 0 π 2 sen ⁡ y d y

Passo 4

Como dividimos em duas integrais, vamos calcular a primeira integral usando substituição simples:

u = cos ⁡ y

d u = - sen ⁡ y d y

Para os limites de integração:

y = 0 → u = 1

y = π 2 → u = 0

A integral fica:

∫ 0 π 2 sen ⁡ y e cos ⁡ y d y = ∫ 1 0 - e u d u

= - e u 1 0

= e - 1

E pra segunda integral:

∫ 0 π 2 sen ⁡ y d y = - cos ⁡ y 0 π 2

= 1

Voltando, pra achar a resposta:

= ∫ 0 π 2 sen ⁡ y e cos ⁡ y d y + ∫ 0 π 2 sen ⁡ y d y

= e - 1 + 1

= e

Resposta

e

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos ⁡ x1 + cos 2 ⁡ xd xd y
Inverta a ordem de integração.