Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
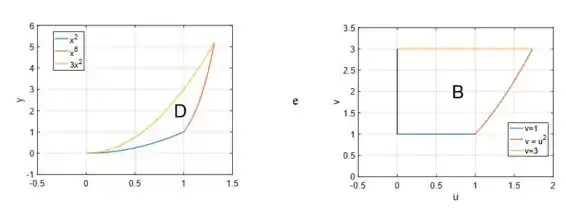
Questão 2: Seja a região do plano e considere a mudança de variáveis ,
- Esboçar e a região do plano tal que ;
- Calcular
Passo 1
Bem, vamos começar o problema desenhando a região mais fácil de desenhar que é a própria região . Ela é mais fácil de desenhar porque já temos aqui a função de todas as curvas que delimita ela:
Duas parábolas (no primeiro quadrante por que só queremos os pontos de que tem ):
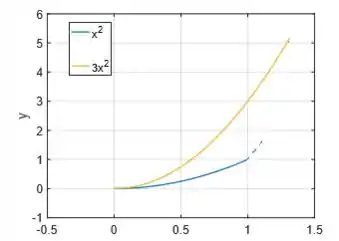
A última curva que delimita a região é (uma espécie de parábola só que mais íngreme):
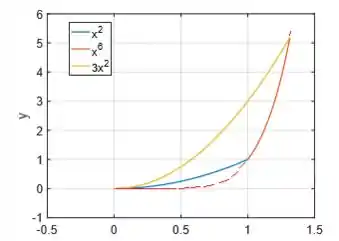
Assim, concluímos que a região é a região do interior dessas três curvas:
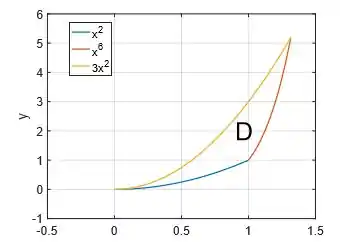
Passo 2
Agora vem uma parte um pouquinho mais chata: desenhar a região ! Ela é um pouquinho mais chat, porque ao contrário da região , que já tinha as equações das curvas que a delimitava, essa região , ainda não tem, e essa será a nossa primeira tarefa: determinar os limites de .
Ok, então vamos nessa: a única coisa que sabemos da região é que:
Isso significa que se pegarmos pontos da região e aplicar na transformação, isso tem que me gerar pontos da região :
Como ...
Por igualdade de vetores:
E essa, basicamente é a nossa mudança. Vale ressaltar que isso acontece com todos os pontos de . Então, se isso acontece com todos os pontos, isso acontece com a fronteira de também, concorda?
Como a fronteira são três equações: , para cada curva dessas vamos ter que resolver um sistema diferente. Por exemplo, se quisermos ver qual é a curva no plano que representa , basta resolver o sistema:
Então a curva no plano que representa é :
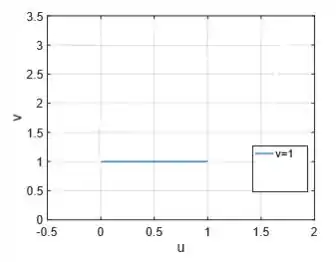
Para a representação de ...
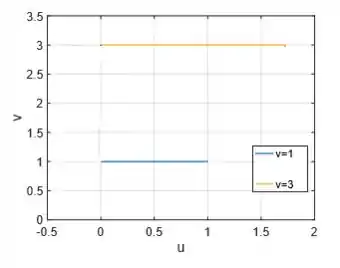
Por fim: ...
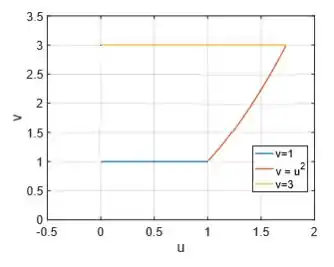
Acabamos de representar as três curvas de no , mas veja que ainda não temos uma região , afinal de contas esse cara está aberto, então venha comigo para vermos como vamos fechar!
Passo 3
Bem, uma coisa que não podemos esquecer é que e tem um vértice em comum no ponto :
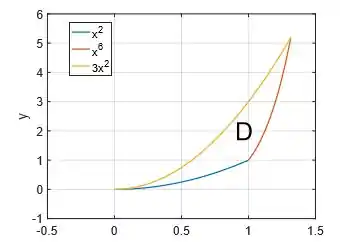
Se substituirmos esse ponto nos dois sistemas que descobrimos essas curvas:
Isso significa que a transformação , leva o ponto em um valor de :
Observe que o valor de não importa se , afinal, da segunda equação:
Então, a representação do ponto no plano é uma reta onde e é um termo independente:
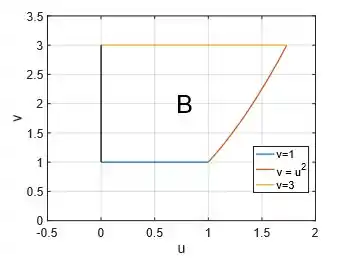
Sacou?
Passo 4
Vamos recapitular o que nós queremos aqui, e o que nós queremos mesmo é resolver a integral dupla:
Muitos poderiam pensar: “Hum... Uma integral dupla na região ... Basta descrevê-la e sair integrando”. Mas veja você que a região é muito complicada:
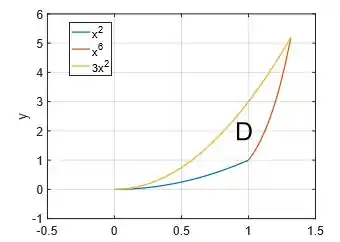
Mas veja que temos uma solução bem legal vinda do item ... Vamos utilizar a mudança de variáveis e utilizar a região em e que é bem mais simples:
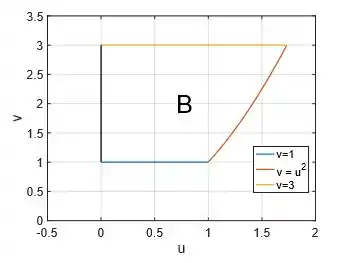
Passo 5
Beleza, a mudança que vamos fazer é a mudança do item , ou seja:
O Jacobiano dessa mudança é:
Com essa mudança, a integral dupla que queremos, vira:
Observe que além de substituir e , duas coisas importantes aconteceram (e sempre acontece quando fazemos mudança de coordenadas):
- Trocamos a região de integração por , já que agora estamos trabalhando com uma integral no domínio de e (e só para lembrar, da letra do problema).
- Além disso, multiplicamos a função do integrando pelo Jacobiano !
O que nos falta mesmo, antes de retornar para a integral e arrebentar é só encontrar a descrição da região , ou seja, onde e variam! Bora nessa, então?
Passo 6
Visualizando novamente a região :
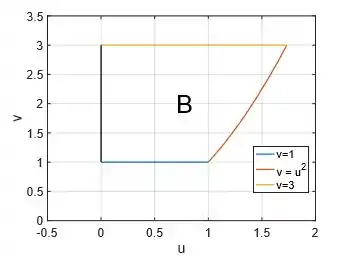
Podemos ver que conseguimos descrevê-la de forma mais tranquila se considerarmos a configuração de tipo 2, ou seja, temos o variando entre intervalos numéricos bem definidos:
Enquanto o varia do lado preto ao outro lado vermelho:
Passo 7
Substituindo então na integral dupla que vamos resolver:
Dando mais uma ajeitada na integral:
Para resolver a integral de dentro (considerando constante), que tal fazermos uma substituição simples:
Lembre-se de substituir também os limites:
Resposta
