Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
UFPE, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº Ricardo F. da Silva - Undécima Lista, Questão 3c
Esboce a região de integração e calcule a integral trocando a ordem de integração.
c)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente trocar a ordem de integração, esboçar a região e calcular a integral. Essa região de integração é definida pelos intervalos da integral dupla que ele nos deu. Nesse caso, temos a região:
Esboçando a região, temos:
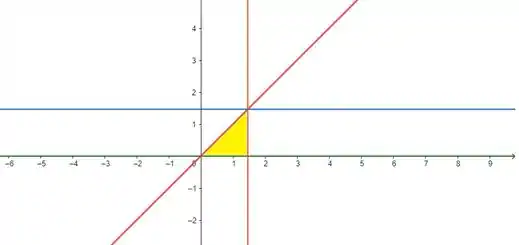
Em vermelho, temos a reta , que também pode ser escrita como . A reta em verde representa e, em laranja e azul, temos as retas e , respectivamente. Se a gente inverter essa ordem de integração, vamos olhar primeiro para , e ver que ele vai ta variando de até a reta . Depois olhando para , vemos que ele vai de até , ou seja:
Dessa forma, vamos resolver a integral:
Vamos lá!
Passo 2
Vamos começar integrando em relação a . Mas antes vamos precisar fazer uma substituição pra facilitar nossa vida. Vamos chamar , assim derivando em relação a , temos:
Além disso, quando , temos e quando , temos . Então, substituindo na integral:
Como a gente tá integrando em relação a e trantando como constante agora, vamos colocar o do lado de fora da integral:
Simplificando a fração do lado de fora e integrando em relação a , temos:
Aplicando os intervalos de integração em :
Passo 3
Agora, vamos integrar em relação a . Mas pra tornar essa integral mais simples, vamos fazer outra substituição, dessa vez chamando . Dessa forma, derivando, temos
Além disso, quando , vamos ter e, quando , vamos ter . Então, alteramos também nossos limites de integração, e nossa integral fica assim:
Colocando a constante pra fora da integral e simplificando o , temos:
Integrando, vai ficar:
Aplicando os intervalos de integração:
Valeu, galera! Até a próxima! 😉