Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
UFF – Cálculo 2 – P2 – Questão 1b
Considere a integral abaixo
b) inverta a ordem de integração
Passo 1
Oi, tudo bem? Vou te ajudar a resolver esse problema, vamos lá? O problema deu essa integral dupla
E pediu para invertermos a ordem de integração. Mas como fazer isso?
Precisamos olhar para os limites dados! Da integral nossos limites são:
E agora vamos colocar esses limites em um gráfico:
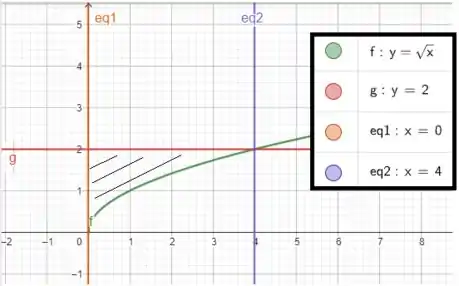
Na integral dada o limite é , então temos que olhamos primeiro no (função mais para cima menos a função que está mais para baixo), já varia de um número a outro. Agora para inverter a ordem vamos olhar primeiro para o : a função mais à direita menos a mais à esquerda, e o é quem vai de um número até outro
Tranquilo?
Partiu começar?
Passo 2
Quando temos nossos limites são
Temos essas equações limitantes aqui
Agora vamos analisar em primeiro:
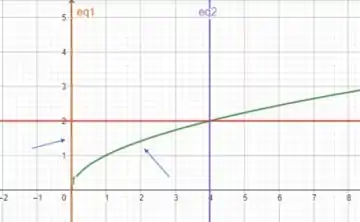
A função mais à direita é , que será nosso limite superior. A função mais à esquerda é , nosso limite inferior. E quanto ? Ele vai de até , como podemos ver pelo gráfico! Assim nossos limites na ordem invertida ficam
Tudo bem até aqui?
E a integral fica
Belezinha?
Até a próxima!