Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas

Ver Teoria
Exercício 71234568910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

Integrais duplas sobre regiões gerais

Inverta a ordem de integração e calcule a integral iterada:

∫ 0 2 ∫ y 2 4 y ln ⁡ ( 1 + x 2 ) 1 + x 2 d x d y

Passo 1

Bom, antes de tudo vamos desenhar essa região de integração para poder visualizar melhor o problema.

Temos x variando desde x = y 2 (uma parábola com eixo de simetria em x ) até x = 4 (uma reta). Enquanto 0 ≤ y ≤ 2 . Portanto, isso aqui:

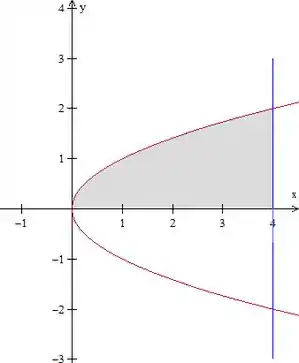
Beleza?

Passo 2

Ok, agora vamos reescrever essa região como tipo I, ou seja, com y variando entra curvas e x entre números.

Bem, y varia desde y = 0 até a parábola x = y 2 . Isolando o y nessa equação, temos y = ± x , mas, como vemos pela figura, só nos importa a parte com y positiva, ou seja, y = x . Podemos escrever então 0 ≤ y ≤ x .

Como vemos pela figura, temos 0 ≤ x ≤ 4 . Passando isso para a integral com a ordem invertida, temos:

∫ 0 2 ∫ y 2 4 y ln ⁡ ( 1 + x 2 ) 1 + x 2 d x d y = ∫ 0 4 ∫ 0 x y ln ⁡ ( 1 + x 2 ) 1 + x 2 d y d x =

Passo 3

Agora é só resolver isso aí.

= 1 2 ∫ 0 4 y 2 ln ⁡ ( 1 + x 2 ) 1 + x 2 0 x d x =

= 1 2 ∫ 0 4 ln ⁡ ( 1 + x 2 ) 1 + x 2 x d x =

Agora vamos fazer a susbstituição:

1 + x 2 = u

2 x d x = d u

x = 0           →         u = 1

x = 4           →         u = 17

Levando para a integral:

= 1 4 ∫ 1 17 ln ⁡ ( u ) u d u =

Agora, fazemos:

ln ⁡ u = v

1 u d u = d v

u = 17           →         v = ln ⁡ 17

u = 1           →         v = 0

= 1 4 ∫ 0 ln ⁡ 17 v d v =

= 1 8 v 2 0 ln ⁡ 17 =

= ln 2 ⁡ 17 8

Resposta

ln 2 ⁡ 17 8

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ a r c t gx π / 4 f x , yd yd x
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Calcule a integral trocando a ordem de integração.49. ∫ 0 1 ∫ a r c s e ny π / 2 cos ⁡ x1 + cos 2 ⁡ xd xd y
Inverta a ordem de integração.