Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
3) Calcule as seguintes integrais:
a)
onde é limitada por .
Passo 1
Pois bem! Em problemas como esse devemos sempre começar fazendo um esboço da região. Mas não se preocupe, pois fazer isso significa colocar no plano todas as curvas dadas.
Vamos começar aqui colocando as mais simples primeiro: e . Ambas nos representam umas retas, onde a primeira, , é paralela a e a segunda a :
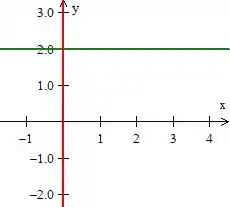
Quanto à segunda equação, , tem o gráfico sendo
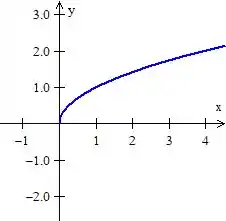
O legal é que já dá pra ver que região estamos trabalhando! :D
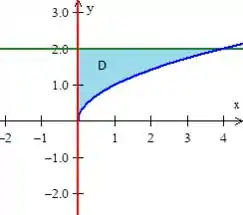
Agora temos que descrever essa região! Bora?
Passo 2
Agora precisamos pensar um pouco: que tipo de descrição podemos fazer de forma que simplifique os cálculos? Do tipo ou do tipo ?
Bem, se fizermos do tipo , quando substituíssemos na integral, como nesse caso variaria entre funções, a integral de dentro seria em :
O que seria impossível com métodos fáceis resolver a integral, a final estaria integrando .
Por isso devemos escolher o Tipo 2. Sacou?
Passo 3
Bem pra esse tipo de descrição, precisamos colocar o variando em um intervalo numérico bem definido.
O que é bem easy, nos bastando observar que varia entre a reta , até a reta verde
Passo 4
Bem...! Quanto à variação do dentro dessa região, ele entra na equação na reta vermelha...
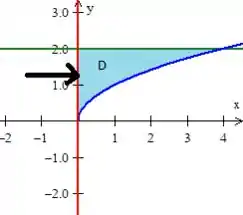
e sai na curva azul
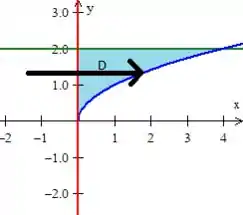
Como a curva azul tem equação
Isolando se o elevando ao quadrado ambos os lados...
Logo...
Passo 5
Podemos então retornar a integral que queremos resolver
e substituir essa integral região por
Mas não se esqueça que o limite numérico sempre vem primeiro :
Bora resolver essa integral aí?
Passo 6
Primeiro calculemos a integral de dentro...
A integral de em termos de é tomado como uma constante, por isso “vaza” da integral de dentro
Integrando a de dentro...
Substituindo os limites de integração em
Essa integral que sobrou é easy, basta fazermos uma mudança do tipo
Não se esqueça de substituir os limites também, heim!
Logo...
Substituindo os limites, lembrando que