Física 3 - UFF; P1 de 2019.2
15 - Considere um bote de fibra flutuando em uma piscina contendo um líquido incompressível, nas situações ilustradas na figura. Em todos os casos o volume de líquido é o mesmo.
- Bote com uma âncora dentro.
- Bote vazio.
- O bote vazio sofre um pequeno acidente e um pedaço de sua borda quebra, cai na piscina e permanece flutuando.
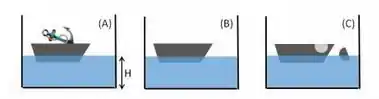
Sendo o nível da superfície do líquido, na situação X (onde X pode ser A, B ou C), medido desde o fundo da piscina, qual das seguintes proposições é a correta?
Passo 1
Ora, a equação que mantêm os três casos os objetos flutuando é a equação que equilibra a força peso com o empuxo:
Onde é a densidade da água e é o volume de água deslocada (que é o volume que sobe por adição do barco menos volume de água total ):
Onde é a área da seção e é o quanto sobe. Já é o peso do objeto...
Logo...
Portanto, será maior quanto maior for a massa boiando na água.
Passo 2
O caso A, possuía a maior massa, logo: é o maior de todos.
O caso e possuem a mesma massa boiando na água (mesmo sendo o caso o caso onde o barco está quebrado, afinal, o pedaço dele caiu na mesma água). Então...
Resposta
Letra C.