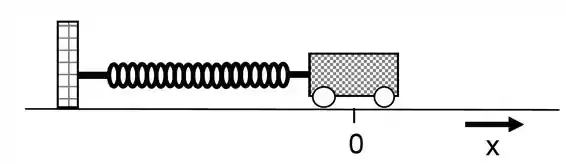
Um oscilador consiste em um bloco de massa preso a uma dada mola. Ao oscilar com amplitude de ele repete seu movimento a cada . Suponha que a posição seja dada por . Se a posição do bloco em é a maior possível, determine:
O período e a frequência angular do movimento;
A constante da mola;
A velocidade máxima e a energia mecânica do oscilador;
A constante de fase ;
Suponha agora que outro oscilador , idêntico ao primeiro e oscilando paralelamente a ele, seja liberado, em , a partir do repouso na posição .
Escreva as expressões e , das posições dos osciladores, e represente num mesmo gráfico essas funções para .
Encontre as duas posições em que eles se cruzam.
Passo 1
O período é o tempo necessário para que um ciclo se complete, pelo enunciado, temos que:
A gora que temos o período, determinar a frequência angular é fácil, se liga:
Passo 2
Agora que temos a frequência angular, determinar a constante elástica é tranquilo, basta lembrar que:
Substituindo, temos
Passo 3
Para determinar a velocidade máxima do oscilador, precisamos lembrar como funciona esse negócio! O oscilador, quando em posição de mínimo ou máximo, tem que sua energia mecânica é puramente elástica:
E valerá:
Quando o oscilador estive passando por , temos que a energia mecânica será puramente energia cinética, e valera:
Substituindo, temos:
Passo 4
Para determinar a constante de fase, vamos primeiro determinar a função . Das informações que já temos, fica:
O enunciado nos diz que para , é máximo, ou seja:
Passo 5
Agora que já temos a função , porque achamos no item anterior, basta achar , moleza! Simbora então!
Como temos que o oscilador é idêntico ao primeiro, já sabemos a amplitude e a frequência angular, basta determinar a constante de fase. A função fica:
Vamos determinar a constante de fase da mesma maneira que no item anterior, ele diz no enunciado que para , temos , substituindo, temos:
Agora sim, temos as duas funções:
O gráfico das duas funções deve ficar assim:
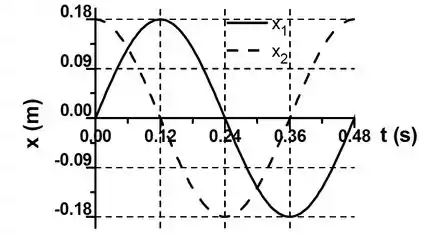
Passo 6
Para determinar os pontos em que os osciladores se cruzam, precisamos satisfazer à seguinte equação:
Assim, iremos achar os tempos em que eles se cruzam, depois, basta substituir em uma das funções para determinar a posição, se liga!
Daqui, tiramos que o único tempo possível é:
Para determinar a posição, basta substituir em qualquer uma das duas funções, aqui, vou substituir em !
simetricamente, temos que os osciladores se encontraram em
Resposta