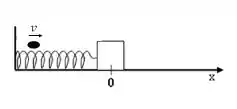
Considere um bloco de massa M preso a uma mola de constante elástica k. O bloco se encontra em repouso quando um objeto de massa m e velocidade v o atinge e se aloja no bloco. Após a colisão, a mola se alonga e o sistema realiza um movimento harmônico simples (MHS). Desprezando a compressão da mola durante a colisão e assumindo t = 0 o instante imediatamente após a colisão, marque a alternativa correta que descreve a solução x(t) do MHS resultante.

a)

b)

c)

d)

e)

f)

g)

h)

i)

Vamos lembrar que a equação do MHS é desse tipo:

E então:

Repare que tanto faz se eu uso seno ou cosseno em ! Porque se eu usar seno, vou achar um determinado valor de . Se eu usar cosseno, vou achar outro valor de . Na prática, não faz diferença, porque os dois resultados expressam o mesmo movimento. Mas, resolvendo a questão antes eu percebi que se usarmos:

Não tem nenhuma alternativa que bata. Então vamos usar seno mesmo. =)

Perceba agora que a velocidade que a gente achou no passo anterior é a velocidade máxima do conjunto! Porque ele tá passando na posição x = 0, equilíbrio, onde a energia cinética é máxima. E a velocidade máxima é:

E ?

Préstenção, a gente calcula do mesmo jeito de sempre:

Mas aí no caso a massa é do conjunto né? Então:

Substituindo:

Vamos perceber agora que:

Então = 0.

Vai ficar então: