Considere um pêndulo constituído de uma mola com uma massa presa na sua extremidade, conforme mostrado na Figura . A mola é disposta de tal forma que fica em linha reta (por exemplo, podemos imaginar que existe uma barra rígida envolvida pela mola). O comprimento da mola é . A mola é então esticada de um comprimento , passando a assumir um comprimento . Ao mesmo tempo, o pêndulo é deslocado de um ângulo com a vertical. Com base nessas informações, considere as alternativas a seguir.
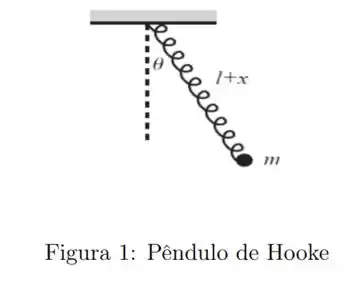
Mostre que a lagrangeana correspondente ao sistema dado é
Passo 1
Oiie, tudo certinho?
A seguinte figura é um bom resumo de nosso enunciado
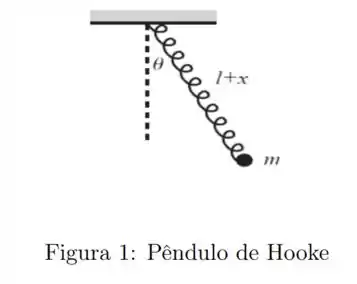
uma massa presa a uma mola que oscila em um pêndulo. Estamos considerando que a mola não se curva, apenas se estica, e as condições em um instante qualquer de tempo são que ela está em um posição angular e esticada de . Tanto quanto são funções do tempo, sabendo isso, como podemos construir a lagrangeana pedida? Parece assustador, mas é simplesmente aplicando a definição
em que é a energia cinética, e é a energia potencial em relação a um referencial! Vamos tentar fazer isso! Vem comigo!
Passo 2
A massa tem energia cinética dada por
note que a velocidade é a derivada das coordenadas da partícula no tempo, em nosso caso, temos que as coordenadas podem ser escritas em termos do ângulo como
e
tome cuidado para não confundir e , é a horizontal de um referencial, e é a mola sendo esticada. Se derivarmos ambos os vetores em relação ao tempo, temos as seguintes expressões
e, da mesma forma, temos que
A velocidade é a soma dos dois coeficientes acima ao quadrado, temos que
expandindo os produtos e simplificando termos, temos que
e, a energia cinética é dada simplesmente por
Note que foi preciso usar a identidade . Vamos escrever a nossa energia potencial agora!
Passo 3
A energia potencial depende do referencial, para ficar mais simples de visualizar, eu escolhi um referencial da forma
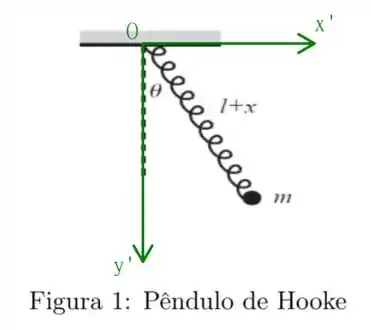
neste caso teremos que a energia potencial é a combinação de dois termos, a energia potencial gravitacional e a energia potencial elástica devido a mola. A primeira é dada por
O sinal negativo na fórmula é consequência do teorema do trabalho e energia, note que a energia tem que diminuir quando eu vou para valores maiores de (em minha escolha que aponta para baixo). A energia potencial elástica de uma mola depende do quanto ela está esticada, da seguinte maneira
em que é simplesmente o deslocamento da mola! Sendo assim, a nossa energia potencial é dada por
e, finalmente, a lagrangeana pode ser escrita como
A primeira alternativa foi isso! Te vejo na próxima!
Resposta
Ao longo dos passos!