Uma barra delgada e homogênea de massa M possui um pivô em uma das extremidades e na outra, uma mola vertical de constante elástica k. Mostre que a barra, quando deslocada de um pequeno ângulo de sua posição de equilíbrio horizontal e liberada, realiza um movimento harmônico simples de frequência angular .
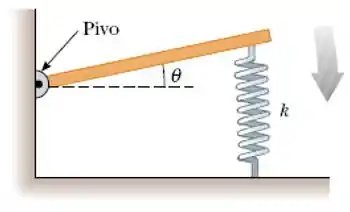
Passo 1
Primeiro vamos considerar a posição de equilíbrio!
Na posição de equilíbrio, a mola está relaxada. Então ela não vai tá fazendo nenhuma força ou momento na barra. Beleza?
Vamos fazer o somatório de momentos no ponto de encaixe do pivô, no equilíbrio. Vou chamar o comprimento da mola de L. Vamos ter:
Ou seja: no ponto de apoio do pivô ele vai tá exercendo um torque sobre a barra que vale o oposto do torque da força peso na posição de equilíbrio.

Passo 2
Show! Agora vamos aplicar a segunda lei de Newton para rotações no ponto de encaixe do pivô.
O torque da força peso vai ser:
O torque do pivô vai ser:
E o torque da força elástica? Vai ser:
E nós podemos dizer que x, que é a elongação da mola, é:
Maravilha! Uma observação: estamos considerando como negativos os torques que fazem a barra girar no sentido horário e como positivos os torques que fazem ela girar no sentido anti-horário.
Passo 3
Agora vamos aplicar a segunda lei de Newton para rotações.
Vai ficar:
Como são pequenas inclinações podemos dizer que:
E para a barra, a inércia é:
Trocando:
Comparando com o MHS:
Resposta
Demonstração! 