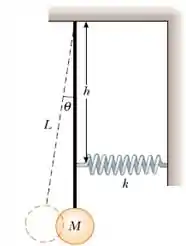
Um pêndulo é constituído por uma partícula de massa M pendurada na extremidade de uma barra rígida fina de massa desprezível e comprimento L. Uma mola de constante elástica k é conectada à barra a uma distância h abaixo do ponto de suspensão, conforme a figura abaixo. Encontre a frequência angular do sistema para valores pequenos da amplitude .
Passo 1
Aqui a gente vai ter que usar a segunda lei de Newton para rotações. É aquela que em vez de força resultante, a gente usa torque resultante.
Em um pêndulo igual a esse da figura, a força peso se decompõe assim:
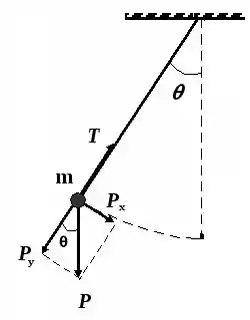
E a única força que vai tá fazendo torque, além da força elástica, vai ser essa força . Porque a outra parte do peso, paralela ao fio, não produz torque. Beleza?
E nós podemos escrever que:
Coloquei esse sinal de menos porque a gente tá considerando como negativo tudo que faz esse cara girar no sentido anti-horário!
Então o torque da força peso vai ser:
Passo 2
Para a força elástica vamos ter:
E como esse x é a compressão da mola, podemos aproximar que:
Então:
E o torque da força elástica então vai ser:
Passo 3
Aplicando a segunda lei e Newton para rotações:
A inércia do pêndulo simples é:
Então:
E como ele disse que são pequenas inclinações, podemos dizer que:
Então:
Passo 4
Lembra da equação do MHS, que é:
Então: