Considere o movimento harmônico simples de um bloco de massa ligado a uma parede vertical através de uma mola de constante elástica , como ilustrado na figura abaixo. Não há atrito entre o bloco e o plano horizontal e nem há resistência do ar neste ambiente. Sabe-se que no instante o bloco está na posição , onde a deformação da mola é máxima. Nestas circunstâncias, calcule:

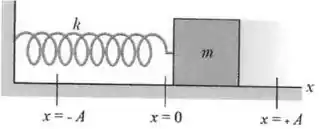
1. O valor da constante de fase deste movimento harmônico simples.
2. O instante de tempo para o qual a posição do bloco é .
3. O instante de tempo para o qual a energia potencial elástica da mola é igual da energia mecânica do sistema em .

A letra (a) pede o valor da constante de fase ().

Em . Assim, usando a nossa equação do passo 1, temos:

Com isso, .

Como , temos que:

Na letra (b), ele nos pede o instante de tempo para , então:

Dessa forma:

Mas como:

Sabemos que a energia elástica () é dada por:

Como e a energia mecânica do sistema é igual a energia potencial elástica:

Como na letra (c) ele quer o instante de tempo em que a energia potencial elástica é igual a da energia mecânica, que é a própria energia elástica, do sistema em :

Com isso:

E: