
Passo 1
Como a rapidez máxima foi dada podemos calcular a energia máxima do sistema
Outra forma de calcular essa energia máxima é através da energia máxima elástica
Passo 2
Como se trata de um movimento harmônico, podemos escrever a trajetória da seguinte forma.
Como ele quer saber o tempo em , ele quer que o t) seja , ou seja.
Mas a gente precisa descobrir antes quanto vale o , pra isso vamos usar dados que o enunciado já deu pra gente
Sendo assim já podemos encontra o
Passo 3
Como se trata de uma colisão elástica, podemos considerar que há conservação tanto do momento linear do sistema quanto da energia cinética, sendo assim, a amplitude máxima também se conserva.
Passo 4
Essa questão da frequencia angular vai ser a mesma ideia que nós usamos na letra b dessa questão, a única diferença é que agora temos duas massas na mola, e não uma só
Resposta
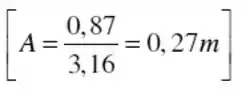
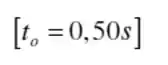
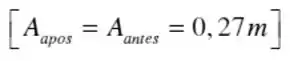
![]()