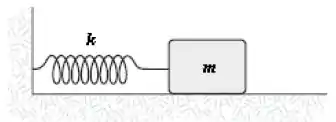
O bloco de massa está acoplado a uma mola de constante elástica como na figura. O bloco é deslocado para a direita sobre uma superfície perfeitamente lisa, esticando a mola de , e posteriormente é abandonado a partir do repouso. Qual das funções abaixo descreve o movimento oscilatório deste bloco sobre o eixo x, orientado para a direita, com origem na posição de equilíbrio do bloco?
(A)
(B)
(C)
(D)
(E)
Passo 1
A posição de um movimento harmônico pode ser escrita com:
Onde é a amplitude, é a frequência angular e é a diferença de fase.
Vamos achar cada um deles.
Passo 2
O enunciado diz a mola é esticada e depois o bloco é solto.
Então, esse é o limite máximo que o bloco alcança, ou seja a amplitude:
Temos:
Passo 3
A frequência angular é dada por:
Simm... é uma boa você gravar essa expressão, pois ela sempre aparece nas questões de MHS.
Substituindo os valores, temos:
Logo:
Passo 4
Agora, só falta a fase .
No instante inicial, o bloco está na posição máxima . Então:
Logo:
Então, nossa expressão ficou:
Ficamos com a letra (B).
Resposta
Letra (B)