A figura abaixo mostra os gráficos da energia cinética K em função da posição x para três osciladores harmônicos que têm a mesma massa. Ordene os gráficos de acordo com a constante elástica dos osciladores, começando pela maior.
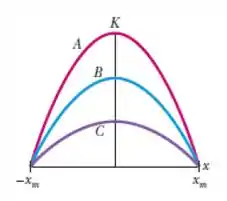
a) A, B, C;
b) B, A, C;
c) C, B, A;
d) A, C, B;
e) C, A, B;
Passo 1
Primeiro nós temos que perceber que a energia cinética máxima vai ser igual à energia potencial máxima! Na energia potencial máxima, a energia cinética é zero, e vice versa!
Então:
Pra uma amplitude fixa, k vai ser maior quanto maior for a energia cinética.
As energias cinéticas são, em ordem crescente:
Então a constante elástica k, em ordem crescente, vai ser:
Resposta
Letra A.
Exercícios de Livros Relacionados
Na figura, um bloco pesando 14,0N , que pode deslizar sem atrito em um plano inclinado de ângulo θ = 40,0 ° , está ligado ao alto do plano inclinado por uma mola de massa desprezível de 0,450m de comp
Um oscilador é formado por um bloco preso a uma mola ( k = 400N / m ). Em um certo instante t , a posição (medida a partir da posição de equilíbrio do sistema), a velocidade e a aceleração do bloco sã
Um bloco de 1,2k g deslizando em uma superfície horizontal sem atrito está preso a uma mola horizontal com k = 480N / m . Seja x o deslocamento do bloco a partir da posição na qual a mola se encontra
A figura mostra uma massa de 1,0k g colocada sobre uma massa de 5,0k g que oscila sobre uma superfície sem atrito. A constante elástica é de 50N / m , e o coeficiente de atrito estático entre os dois
A figura mostra um bastão homogêneo de 200g com um orifício em uma das extremidades. A outra extremidade é presa a uma mola horizontal. Quando o bastão está suspenso exatamente na vertical, a mola não