Considere um pêndulo constituído de uma mola com uma massa presa na sua extremidade, conforme mostrado na Figura . A mola é disposta de tal forma que fica em linha reta (por exemplo, podemos imaginar que existe uma barra rígida envolvida pela mola). O comprimento da mola é . A mola é então esticada de um comprimento , passando a assumir um comprimento . Ao mesmo tempo, o pêndulo é deslocado de um ângulo com a vertical. Com base nessas informações, considere as alternativas a seguir.
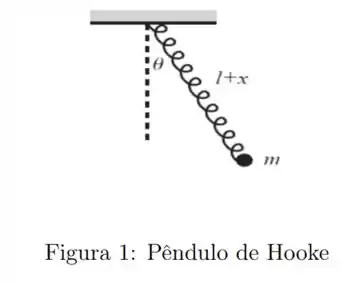
Obtenha as equações de movimento relativas às coordenadas e .
Passo 1
Oiie, tudo certinho?
A seguinte figura é um bom resumo de nosso enunciado
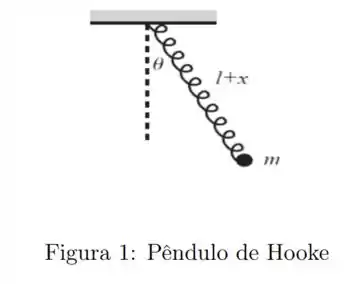
uma massa presa a uma mola que oscila em um pêndulo. Estamos considerando que a mola não se curva, apenas se estica, e as condições em um instante qualquer de tempo são que ela está em um posição angular e esticada de . Tanto quanto são funções do tempo, na alternativa anterior obtemos a lagrangeana como
obter as equações de movimento é o mesmo que dizer “aplique as equações de Euler-Lagrange”, elas são da forma
em nosso caso temos que , que são as nossas coordenadas independentes! Vamos obter então duas equações independentes! Saca só!
Passo 2
Primeiro, usando , temos que
A derivada parcial em relação a de nossa lagrangeana é
note que zerei termos que não dependem explicitamente de (isso incluí , já que a velocidade no formalismo lagrangeano é considerada uma variável independente). Aplicando a regra da cadeia e algumas regrinhas básicas de derivação, temos que
Da mesma maneira, precisamos calcular a derivada parcial em relação a , obtendo
calculando então a derivada total
obtemos
Finalmente, a nossa primeira equação do movimento é dada por
Vamos calcular a outra agora! Vem comigo!
Passo 3
Temos que repetir todo o processo para , temos então a seguinte equação
primeiro calculando a derivada parcial em , temos que
a derivada parcial em relação a é dada por
agora, com um pouco mais de trabalho, precisaremos calcular a derivada total
usando a regra do produto e a regra da cadeia, temos que
Nossa equação do movimento é simplesmente
simplificando, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e