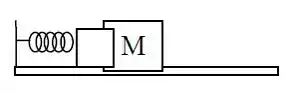
Um bloco de massa m está sobre uma superfície horizontal e preso a uma mola ideal de constante elástica k. Outro bloco de massa M é encostado no bloco m, como mostra a figura, e empurrado de modo a comprimir a mola de X. Nesta posição, o sistema é abandonado do repouso e desliza sobre a superfície sem atrito. Dados: X = 10,0 cm e M = 3 kg.
a) A partir de qual posição um bloco perderá o contato com o outro?
b) Qual a distância entre os blocos quando o bloco m atingir o repouso pela 2a vez após a perda de contato com M?
Passo 1
a) Então, depois que os blocos são abandonados eles vão juntos até a posição de equilíbrio, onde atingem a velocidade máxima. A partir de então o bloquinho preso à mola começa a desacelerar, por causa da força elástica, e o blocão continua com a velocidade máxima que eles atingiram no equilíbrio. Então é a partir da posição de equilíbrio que eles começam a perder o contato.
Passo 2
b) Na posição de equilíbrio, quando começam a perder o contato, a velocidade dos blocos é máxima! A energia cinética também é máxima, e ela vai ser igual à energia mecânica do sistema. Então:
Repare que a amplitude é igual ao X que ele fala no enunciado, que é a posição em que o sistema é abandonado.
Passo 3
Achamos a velocidade máxima no passo anterior. O blocão vai seguir nessa velocidade constante após perder o contato com o bloquinho. Beleza?
E a distância que ele vai percorrer nesse tempo vai ser:
Então falta achar esse tempo t!
Pensa comigo. Depois de passar do equilíbrio (se soltando do blocão) o bloquinho segue até uma extremidade (na mesma direção que o blocão tá indo), atinge velocidade igual a zero e volta na direção contrária. Oscilando, não é mesmo?
Depois o bloquinho atinge a extremidade contrária, de onde ele foi abandonado, e atinge velocidade zero de novo.
Essa é a segunda vez que ele atinge o repouso!
Então quantas oscilações o bloquinho faz nesse tempo? Bom, em um período completo (uma oscilação) o bloquinho sairia do equilíbrio, iria até uma extremidade, voltaria até a outra extremidade e chegaria no equilíbrio de novo completando um período.
Mas nós só queremos que ele saia do equilíbrio, vá até uma extremidade e volte pra outra extremidade de novo. Ou seja, ele vai ta completando ¾ de oscilação! E vai fazer isso em ¾ de período!
Então o nosso tempo vai ser:
Passo 4
Substituindo a fórmula do período:
Beleza!
E qual vai ser a distância entre os blocos então? Vai ser a distância S que o blocão percorreu no tempo t, mais 10 cm. Dá uma olhada nessa figura:
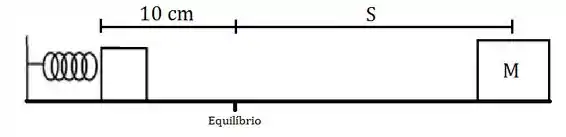
Então vamos achar S!
Substituindo t:
E trocando :
A distância entre os blocos vai ser: