Calcule o limite:
Passo 1
A gente começa substituindo o limite, certo?
Deu ruim né? Então, vamos tentar usar uma malandragem algébrica.
Passo 2
Zerou em cima e embaixo, o que significa que vai aparecer na fatoração dos dois termos. Vamos dividí-los por esse termo, o de cima por Briot-Ruffini, o de baixo por Bhaskara.
Começamos com o de baixo:
Ou seja, .
OBS.: Esse aí veio por que nesse polinômio.
Passo 3
O de cima, dividimos ele por pelo método de Briot-Ruffini:
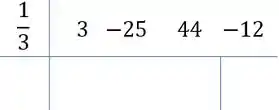
Desce o primeiro coeficiente:
Multiplicamos a raiz pelo primeiro e somamos ao segundo:
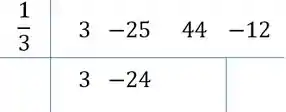
Repetimos isso para os dois outros números que restam:
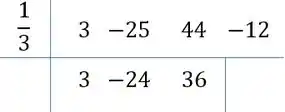
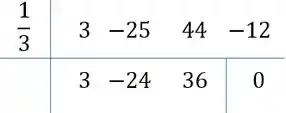
Ou seja, .
Passo 4
Substituindo no limite:
Na divisão de 2 frações, repetimos a primeira e multiplicamos pelo inverso da segunda:
Aplicando o MMC, achamos que:
Resposta
Exercícios de Livros Relacionados
Existe um número a tal que lim x → - 2 3 x 2 + a x + a + 3 x 2 + x - 2 exista? Caso afirmativo, encontre a e o valor do limite.
Calcule o limite, se existir. lim h → 0 ( 3 + h ) - 1 - 3 - 1 h
Calcule o limite, se existir. lim x → 1 x 3 - 1 x 2 - 1
Determine o limite infinito.underset(x - pi^-)(lim) cot x
Calcule o limite, se existir. 12 . lim x → - 4 x 2 + 5 x + 4 x 2 + 3 x - 4