Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Passo 1
Subsituindo o você já percebe logo de cara que esse cara vai para uma indeterminação:
Bom, pra fugir disso a gente precisa fatorar esse cara. Mas calma aí, o bagulho tá elevado a ? Como eu faço isso??
Então, você não faz! Mas nós marotamente faremos algo que vai nos levar ao resultado, através de um padrão na fatoração.
Passo 2
Lembra que a dica para fatorar polinômios de grau maior ou igual a era usar Briot-Ruffini? Vamos lançar desse jeito então, tendo que o valor é e temos que dividir os dois polinômios por .
Repara ainda, para o polinômio de cima, que teremos no coeficiente de , em todos do grau até , no grau e o . Armando para o cara de cima fica assim:
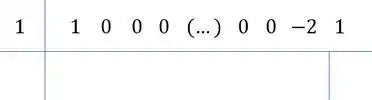
Mesmo esquema, desce o primeiro coeficiente, multiplica ele pela raiz, soma com o próximo coeficiente e assim por diante:
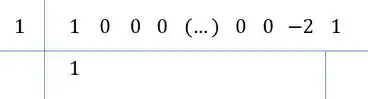
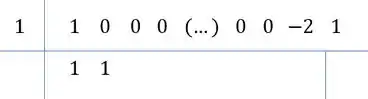
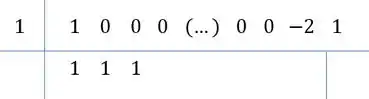
Repara, tem um padrão! Todos com ali vão ter coeficiente ao dividir!
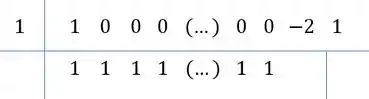
Continuando teremos:
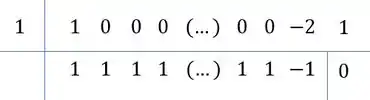
Ou seja, .
Passo 3
Não sei se você já se deu conta, mas para o cara debaixo, com o , vamos ter a mesma coisa! A diferença nesse caso é que os coeficientes zerados estarão só de até . Briot-Ruffini neles!
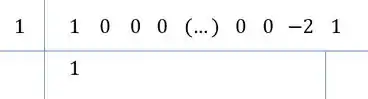
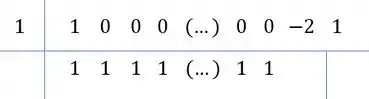
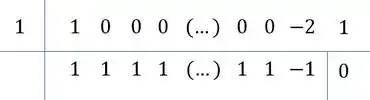
Ou seja,
Passo 4
Substituindo no limite, teremos:
Rapaz, repara nesse limite que sobrou! Lembra que elevado a qualquer número vai dar ? A gente vai ficar com números em cima e embaixo ao substituir , fora os dois que sobraram ali:
Questão trabalhosa e complicadinha, heim?