UFCG – Sem campus – Cálculo Diferencial e Integral I – Listas de cálculo 1 – UAMat – Lista 1 – Limite e continuidade – 10l
Calcule os limites
l)
Passo 1
Opa meus lindos!! Vamos pra mais uma questão. A questão pede pra gente resolver o seguinte limite:
Ué, sem problemas! Vamos aplicar o limite e investigar o que acontece:
Aplicando
Eita, estamos em uma indeterminação... e agora? Calma, vamos analisar o problema. Temos uma divisão de dois polinômios:
E que quando levados ao valor de , ambos polinômios retornam pra gente o valor . Isso significa uma coisa muito útil pra gente: é raiz de ambos os polinômios. Mas, no que isso ajuda a gente? Veja, a gente pode reescrever esses dois polinômios sabendo que é uma das raízes, isso vai ajudar bastante para mudarmos a cara do nosso limite e fugirmos da indeterminação!
Passo 2
Aqui no numerador, as coisas são um pouco mais trabalhosas. O que rola é o seguinte: já que sabemos uma das raízes e precisamos reescrever esse polinômio em um outro formato:
Sendo um polinômio de grau 5 e um polinômio de grau 4.
Lembrando que sabemos quem é , que representa uma das raízes da função. E achamos que , portanto:
E olha que bacana fica o nosso limite:
Desenvolvendo ele:
Agora só precisamos achar quem é esse . Sabe qual o método que vamos usar para encontra-lo? O método que vai nos mostrar como acontece isso é o método de Briot-Rufini. Se liga que vou te mostrar como ele funciona no próximo passo!
Passo 3
Primeiro passo do Briot-Rufini é armar ela. Se temos uma equação do tipo:
E já sabemos uma das raízes , podemos montar da seguinte forma:
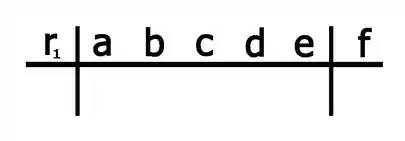
Como nosso polinômio é:
Temos que os coeficientes são:
Montando no Briot-Rufini:
Show, e agora vem a dinâmica: Primeira coisa é descer o primeiro coeficiente!
Agora, para encontrarmos os prótimos coeficientes, realizaremos:
O produto do último novo coeficiente que achamos, com a raiz , somados com o prótimo coeficiente.
Pra ficar mais fácil, visualmente temos:
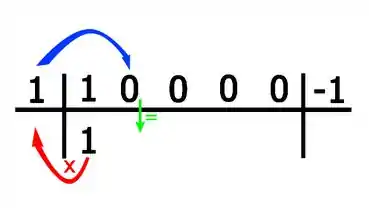
Ou seja:
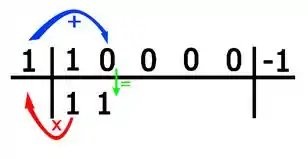
E por aí vai. Continuando o método:
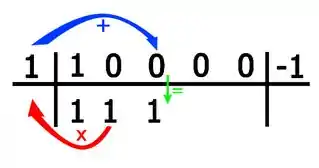
Para o próximo coeficiente:
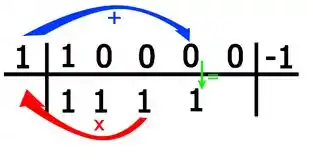
Para o próximo coeficiente:
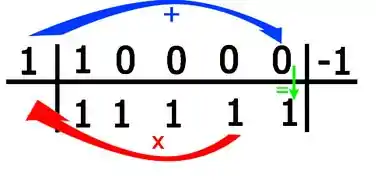
E por fim para a constante:
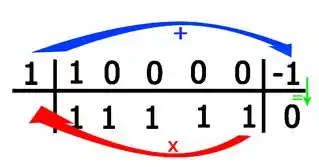
Belezura, de posse desses novos coeficientes , podemos escrever uma nova função da forma:
Usando os novos coeficientes que obtemos do método:
Ou seja, nosso limite agora é:
Resolvendo:
Ou seja:
E é isso gente boa, matamos a questão! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você