UFCG – Sem campus – Cálculo Diferencial e Integral I – Listas de cálculo 1 – UAMat – Lista 1 – Limite e continuidade – 10k
Calcule os limites
k)
Passo 1
Oi galerinha, tudo certo com vocês? Vamo que vamo pra mais uma questão! A questão nos entrega esse limite:
E pede pra gente resolver. Sem muitas delongas, vamos aplicar o valor que o limite nos entrega e ver o que acontece.
Aplicando :
Caímos em uma indeterminação, botam fé? Mas sem pânico... vamos tentar sair dela!
Passo 2
O mais importante aqui nessas questões de limites, é a gente saber várias artimanhas para manipular nossas funções e fugir da indeterminação. Vamos olhar aqui pra o limite da questão:
Mas gente, vocês estão vendo o que estou vendo? Podemos aplicar uma regrinha muito comum em polinômios que é:
Justamente na função . Aplicando isso, para :
Temos então que:
Portanto:
Reescrevendo no nosso limite:
Passo 3
Tranquilo! E olha que legal: podemos refazer esse processo e simplificar mais ainda a nossa função! Tomando dessa vez :
Aplicando isso, para :
Temos então que:
Portanto:
Reescrevendo no nosso limite:
E nosso limite ficou mais simplificável ainda! Conseguimos sumir com aquele termo do denominador! Tomando:
Simplificamos:
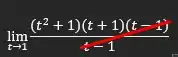
Portanto:
Aplicando o valor do limite para
Ou seja:
E é isso gente boa, matamos a questão! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você