UFCG – Sem campus – Cálculo Diferencial e Integral I – Listas de cálculo 1 – UAMat – Lista 1 – Limite e continuidade – 10f
Calcule os limites
f)
Passo 1
Opa, tudo bem contigo? Vamo que vamo resolver uma questão de limite. Nela, nos é apresentado o seguinte limite:
Uma divisão de polinômios, belezura. Bora aplicar o limite da forma como está e ver o que acontece? Temos que:
Como temos tendendo a , vamos substituir o valor de por . Então, aplicando:
Ora, caímos em uma indeterminação! Vocês lembram mais ou menos o que isso significa? São situações matemáticas que não fazem sentido numericamente. Trazendo pro nosso caso, como encontramos a razão de por , precisamos encontrar um jeito de sair dela. Mas como estamos trabalhando com polinômios, aí vem uma dica de ouro: sempre procure deixar o polinômio do numerador e/ou denominador de outra forma, a fim de tirar a indeterminação do denominador igual a 0.
Ou seja, temos que achar algum jeito de o nosso numerador se simplificar com o denominador, dessa forma conseguiremos sair da indeterminação! E aí, conseguimos, novamente, aplicar o limite até encontrar o valor que queremos. Vamo que vamo!
Passo 2
Show, então nosso limite tem essa cara:
E se a questão nos deu que o denominador é , devemos então dar uma forma de simplificar o numerador de forma que em cima apareça também um . Isso significa que pra questão desenvolver, alguma das raízes do numerador é . E então, a gente consegue fazer algo na forma de:
Entenderam a ideia? Então vamo lá! A gente tem um numerador de grau 4, e intuitivamente sabemos que uma das raízes do numerador é 2, pois ele tem que aparecer na forma:
Pra conseguirmos simplificar o denominador. Sendo e polinômios de grau e respectivamente. E uma técnica que ajuda a gente nesse caso é a técnica de Briot-Rufini. Através dela, conseguiremos achar o formato de , e desenvolver o limite. Você sabe como a gente aplica ela? Vamo lá!
Passo 3
Primeiro passo do Briot-Rufini é armar ela. Se temos uma equação do tipo:
E já sabemos uma das raízes , podemos montar da seguinte forma:
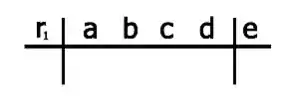
Como nossa função
Temos que os coeficientes são:
Isso, porque temos acompanhando de o número , não temos o termo de , temos , não temos o termo e temos, por fim, acompanhando o polinômio, a constante .
Montando no Briot-Rufini:
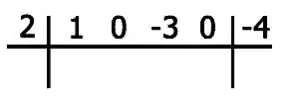
Show, e agora vem a dinâmica: Primeira coisa é descer o primeiro coeficiente!
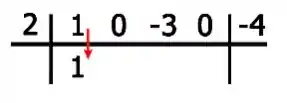
Agora, para encontrarmos os próximos coeficientes, realizaremos:
O produto do último novo coeficiente que achamos, com a raiz , somados com o próximo coeficiente.
Pra ficar mais fácil, visualmente temos:
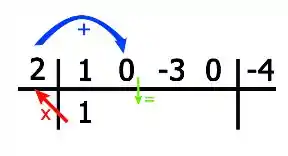
Ou seja:
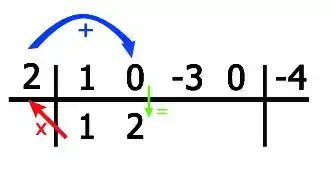
E por aí vai. Continuando o método:
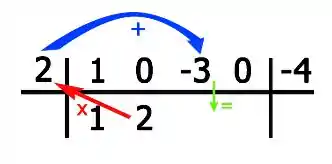
Para o próximo coeficiente:
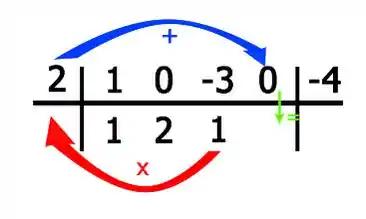
E por fim para a constante:
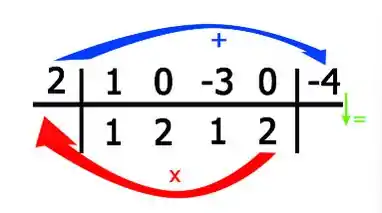
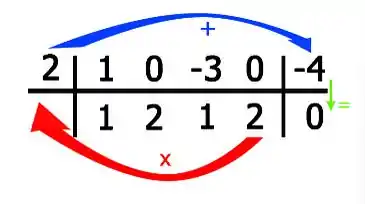
Belezura, de posse desses novos coeficientes , podemos escrever uma nova função da forma:
E lembra lá do passo 2, quando escrevemos que ?
Como temos , então, nossa função
Pode ser reescrita da forma:
E olha que coisa linda, conseguimos simplificar!
Passo 4
Nosso limite no começo era:
Com a última simplificação que fizemos, passou a ser:
Agora a gente consegue simplificar numerador com denominador! Vocês conseguem encontrar alguma semelhança entre eles? Isso mesmo!! Temos em baixo e em cima na equação. Justo do jeitinho que prevemos no Passo 1. Vamos simplificar eles, obtendo:
E aplicando o limite, substituindo por :
Então
Ou seja,
E é isso gente boa, matamos a questão! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você