Exercícios Resolvidos de Classificação de Pontos Críticos em Funções de 2 Variáveis
Ver TeoriaEnunciado
UFF, Sem Campus, Cálculo IIB, 2ª VE - Prof. Sérgio Almaraz - 2014.2, Questão 3b.
3 - Considere a função e a região .
(b) Encontre os máximos e mínimos de em .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão temos que obter os pontos máximos e os pontos mínimos de dentro da região .
Como podemos fazer isso? 👀
Lembra que no item anterior definimos como o nível de e definimos para quais valores de a curva estaria sob a região ?
Vamos dar uma olhada nesse passo um pouco mais de perto!
Bora lá! 🤔
Passo 2
Se o nível de uma função é definido como a uma constante, então fizemos pois nem todos os níveis de estariam sob a região e precisávamos encontrar quais os níveis que satisfaziam nosso problema.
Se e , então
Isolando em um lado, temos
Analisando a região pelo gráfico
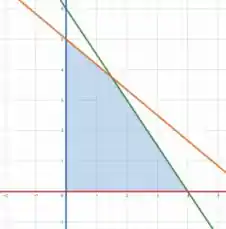
Perceba que em na região , varia de a e em , varia de a .
Como é um plano o valor máximo está no maior nível que encontrarmos nos vértices e de acordo com essas informações varia de a (quando ) e de a (quando ).
Logo, para fazer parte de , temos que pegar o intervalo definido pelo maior valor e pelo menor valor que encontramos para . Que é justamente quando , ou seja, o nível de varia em como
Assim, vemos que o menor valor (menor nível) de em é e o maior valor (maior nível) de em é .
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
O menor valor (menor nível) de em é e o maior valor (maior nível) de em é