Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Classificação de Pontos Críticos em Funções de 2 Variáveis

Ver Teoria
Exercício 391234567891011121314151617181920212223242526272829303132333435363738404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596

Enunciado

Considere

f x , y = y 2 x + x 2 - y 2

  1. Determine conjunto aberto

    2. A = x , y ∈ R 2     h x , y > 0 }  

    explicitando   h ( x , y ) tal que f restrita a A seja estritamente convexa. Exiba a hessiana de f e um ponto Q ∈ A .

  2. Esboce o conjunto aberto A .

Passo 1

a )

Para que f ( x , y ) seja estritamente convexa, precisamos que H ( x , y ) , ou seja, o determinante da matriz hessiana de f , seja estritamente positivo.

Vamos calcular as derivadas primeiras e segundas da nossa função para podermos fazer H x , y > 0 .

f x , y = y 2 x + x 2 - y 2

f x = y 2 + 2 x   ⇒ f x x = 2

f y = 2 y x - 2 y   ⇒ f y y = 2 x - 2

f x y = f y x = 2 y

Passo 2

Assim, temos que a hessiana de f é dada por:

H x , y = f x x f x y f y x f y y

H x , y = 2 2 y 2 y 2 x - 2

Para que ela seja estritamente positiva, precisamos que

f x x = 2 > 0

E

H x , y = 4 x - 4 - 4 y 2 > 0

Como f x x = 2 já é estritamente positivo, então precisamos que

H x , y = 4 x - 4 - 4 y 2 > 0

Assim, o nosso conjunto A é

A = x , y ∈ R 2     h x , y > 0 }  

A = x , y ∈ R 2     4 x - 4 - 4 y 2 > 0 }  

Passo 3

b )

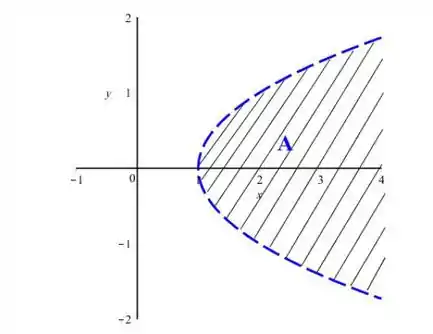
Vamos esboçar o conjunto A .

A = x , y ∈ R 2     4 x - 4 - 4 y 2 > 0 }  

Para isso, vamos desvendar o que que ele representa né? Porque só olhando assim eu nã sei ainda o que é essa equação.

4 x - 4 - 4 y 2 > 0

4 x > 4 y 2 + 4

Dividindo todo mundo por 4:

x > y 2 + 1

E se isso fosse um sinal de igual, assim:

x = y 2 + 1

Teríamos uma parábola “olhando” para o eixo y , cortando o eixo x em x = 1 .

Mas como tem o sinal de maior, significa que estávamos falando de tudo que está maior que a parábola, assim:

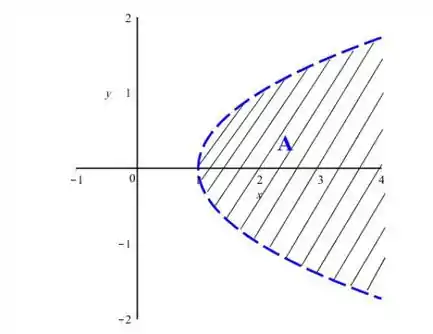
Um ponto Q qualquer que tá aí dentro do conjunto A é, por exemplo, o ponto ( 2,0 ) .

Resposta

a )

A = x , y ∈ R 2     4 x - 4 - 4 y 2 > 0 }  

b )

Q = ( 2,0 ) ∈ A

Exercícios de Livros Relacionados

Mostre que f x , y = x 2 + 4 y 2 - 4 x y + 2 em um número infinito de pontos críticos e que D = 0 em cada um. A seguir, mostre que f tem um mínimo local (e absoluto) em cada ponto crítico.
14.17. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa para traçar gráficos tridimensionais no computador, utilize-o com a janela de inspeção e o po
1. Estude com relação a máximos e mínimos locais a função f x , y = x 3 - 3 x 2 y + 27 y
Utilize um gráfico e/ou curvas de nível para estimar os valores máximos e mínimos locais e pontos de sela da função. Em seguida, use o cálculo para achar esses valores precisamente. f x , y = x y e -