Seja definida no quadrado aberto dado por e .

a) Calcule os pontos críticos de em

b) Classifique os pontos críticos de em

c) Determine um aberto na forma explicitando e satisfazendo as seguintes propriedades:

• A hessiana de em seja estritamente negativa definida.

d) Seja . Calcule o valor máximo e mínimo de restrita à .

Igualando o vetor gradiente que acabamos de encontrar a , temos:

Agora, só precisamos resolver esse sistema! De cara, uma solução possível é colocar para a primeira equação e para a segunda! Mas, infelizmente o ponto não está dentro do quadrado (pois, pela definição do quadrado, e !) então, para nós, ele não serve :/

Nos resta tentar manipular essas equações para ver outras possíveis soluções. Como não vamos colocar um valor fixo para na primeira, podemos dividir todos os termos por , então, teremos:

que fica

Fazendo o mesmo processo para a segunda equação, agora, dividindo por , teremos:

Show? Isso vai nos ajudar muito, por que temos duas equações, com duas incógnitas, e não temos mais nada ao quadrado!

Para resolver o sistema

Podemos multiplicar a segunda equação por

E somar isso na primeira

Show! Acabamos de encontrar um valor para que está dentro dos limites verticais do quadrado! Vamos ver se o também está? Só colocar esse valor encontrado para em qualquer uma das equações. Colocando na primeira, teremos:

E pronto! Temos o ponto , que está dentro do quadrado! Como tínhamos que resolver apenas uma equação de primeiro grau, esse é o único ponto crítico :D

b) Vamos classificar nosso ponto? Para isso, precisamos do determinante da matriz Hessiana:

Para resolver esse determinante, precisamos das segundas derivadas no ponto que encontramos, certo? Partiu encontrá-las! Se tínhamos:

Então,

Colocando o ponto nessas derivadas, temos:

Colocando os valores das derivadas na matriz, teremos:

E aí está! Como temos que o determinante deu mais que , então podemos ter um máximo ou um mínimo. Como a segunda derivada em relação a para o ponto em questão é menor que , , então temos um ponto de máximo!

é ponto de máximo, e vale:

c) Vamos lá, essa é só ter calma pra ler o enunciado. O que temos que fazer é descobrir o conjunto de pontos que está contido no quadrado cujo teste da Hessiana dê sempre negativo. Isso ocorre quando só temos a opção de encontrar pontos de máximo.

Agora é só pensar: o que precisamos para ter um ponto de máximo? Temos que, antes de mais nada, ter o determinante da Hessiana maior que , certo? Depois disso, vemos se a segunda derivada em relação a é menor que .

Vamos separar essas duas condições para ficar mais fácil de visualizar:

• Determinante da Hessiana deve ser maior que .
• Segunda derivada em relação a deve ser menor que .

Olhando para a primeira condição, teremos:

Ou seja, resolvendo o determinante,

Show?

Agora, devemos ver a segunda condição. Ela nos diz que a segunda derivada em relação a deve ser menor que . Logo,

Dividindo os dois lados por ,

Lembrando que quando multiplicamos ou dividimos desigualdades por números negativos, invertemos a boca dela ;)

Como para ser maior que , deve ser maior que também (por causa do ), então basta que essa expressão seja o que a questão pede! Se você não percebesse isso, provavelmente não haveria tanto problema colocar essas duas restrições ;) Nosso subconjunto , fica então:

Ou seja, o conjunto dos pontos tais que tornam o determinante da Hessiana maior que , e a segunda derivada em relação a menor que !

d) Agora chegou a hora de ver os pontos de máximo e mínimo sobre a borda do quadrado! Sim, pois esse conjunto que nos deram é exatamente a definição do nosso quadrado, mas englobando também seu contorno! Como para o seu interior já sabemos que o ponto de máximo é , resta ver se temos algum ponto ainda maior na borda, e verificar qual é o mínimo, também da borda ;)

Ok, e como faremos isso? Basta percorrer cada segmento com a função! Por exemplo, para o segmento , temos constantemente em , e variando entre e !

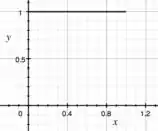
Viu? É a borda superior do quadrado! E como a função se comporta nesse segmento?

Percebe que, como temos variando entre e , o maior valor que a função assume é quando colocamos , que temos ? E o menor valor ocorre quando temos , que é

Agora que você pegou a ideia da coisa, vamos percorrer os outros segmentos vendo os valores que a função assume, para os determinados que colocamos?

Se mantivermos constante, e percorrermos entre e , teremos a outra borda do quadrado:

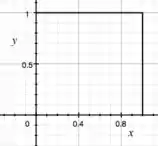
Beleza? E, para a função , teremos:

Ou seja, para , o maior valor assumido é quando , tendo . Enquanto isso, o menor valor assumido é quando temos , para !

Agora, para os outros lados, que estão sobre o eixo e sobre o eixo , que fecham o quadrado, temos:

Pois, em todos os termos de aparece e ao menos uma vez!

Com isso, fechamos todos os valores dentro do quadrado e na sua borda! Lembrando daquele ponto crítico , vimos que , que ainda é maior do que qualquer valor sobre a borda do quadrado. Assim, é o máximo sobre , enquanto é o mínimo.