Seja

Seja

Com

1. Encontre todos os pontos críticos de em .

2. • Encontre um aberto n, tal que restrita à seja estritamente côncava.

   • Exiba um ponto

   • Esboce .

3. Exiba os pontos críticos de em que são pontos de máximo local, justificando sua resposta.

Seja

1. Encontre funções , e tais que a função restrita ao aberto

Seja estritamente côncava. Exiba um ponto .

(Dica: use os calculos do item )

Somando as duas equações:

Mas, como os pontos críticos devem estar dentro de , então o , assim

Substituindo isso na segunda equação:

E não temos nenhuma restrição em relação a no conjunto .

Logo, os pontos críticos são:

Para ser estritamente côncava, isto é para que tenha apenas pontos de máximo, é preciso que

E que

Para .

Ou seja, o determinante da matriz hessiana (do teste da derivada segunda) tem que ser maior que zero e a derivada segunda em relação a tem que ser menor que zero.

Portanto, temos que calcular as derivadas segundas.

Calculando derivadas segundas:

Substituindo nas condições do passo 3:

E

A interseção dessas duas inequações é

Pois se é maior que , ele também é maior que .

E, como , então .

Assim, nosso conjunto pode ser definido como

Agora precisamos de um ponto que pertença a esse conjunto .

Ora, achamos dois pontos na letra . Vamos ver se algum deles está no conjunto ?

Os pontos que achamos foram

E, se você observar, está, de fato, dentro do conjunto , pois

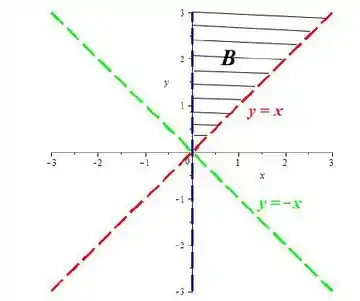
Agora precisamos esboçar o conjunto

Para isso, basta desenharmos as retas

E tracejarmos elas (já que não inclui a fronteira pois não temos sinais de igual). O conjunto será a região entre essas duas retas.

Queremos saber um ponto crítico de em que seja ponto de máximo local.

Bom, na letra a gente calculou os dois pontos críticos de em , mas não classificamos eles, então não sabemos se algum deles é ponto de máximo local.

Maaas, na letra , a gente definiu um conjunto tal que todos os pontos que pertencem a esse conjunto são pontos que fazem com que seja estritamente côncava, ou seja, são pontos de máximo locais.

E, isso mesmo, no passo 6 a gente viu que , logo, é um ponto de máximo local.

O item falou de forma mais confusa, mas no fundo, o que ele quer é que a gente encontre um conjunto para que a função seja estritamente côncava. Ou seja, mesma coisa que fizemos no item , mas agora nossa função tem 3 variáveis e é um pouquinho diferente da função do item .

Mas é só um pouquinho mesmo, olha só:

Basicamente, só trocamos as duas ultimas parcelas de po parcelas que envolvam a variável .

Enfim, de todo modo, vamos seguir o mesmo procedimento da letra do item , o que significa que nossas condições para ser estritamente côncavo são:

E que

Como falamos no passo anterior, é muito parecida com , assim

Fica faltando então só a gente calcular as derivadas em relação a . Vamos fazer:

Substituindo nas condições do passo 9:

Essa parte que está entre colchetes temos que, como condição, ela é maior que zero. Assim, pra isso daí tudo ser menor que zero, temos que ter que

E

Que do item sabemos que vale:

E

Que também do item , sabemos que vale:

Juntando tudo agora, podemos dizer então que se

Então

Agora ainda falta achar um ponto que pertença a esse conjunto.

Se você reparar, esse conjunto é bem parecido com o conjunto que encontramos no item .

A única coisa que muda é que temos a condição de que

Assim, podemos pegar o mesmo ponto que atendia o conjunto e calcular um valor de para ele (pois agora o ponto deve ser 3 coordenadas), de acordo com essa nossa condição.

Assim, se, por exemplo, , teremos que

Então, podemos dizer que o ponto

Pertence ao conjunto .

E, F-I-N-A-L-M-E-N-T-E, acabou!