Exercícios Resolvidos de Classificação de Pontos Críticos em Funções de 2 Variáveis
Ver TeoriaEnunciado
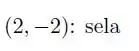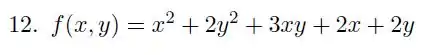
Passo 1
Devemos começar achando os pontos críticos. Primeiro vamos calcular as derivadas da função
Então os pontos críticos são aquele que
Passo 2
Isolando o na primeira equação
E substituindo na segunda,
Assim
O ponto crítico é
Passo 3
Agora devemos calcular o determinante de
Vamos primeiro achar as derivadas segundas
Passo 4
Como nossas derivadas segundas são valores constantes, ao substituir no ponto crítico teremos os mesmos valores constantes.
Assim, o determinante é
Como
Então o ponto crítico é um ponto de sela.
Resposta
Exercícios de Livros Relacionados
Mostre que f x , y = x 2 + 4 y 2 - 4 x y + 2 em um número infinito de pontos críticos e que D = 0 em cada um. A seguir, mostre que f tem um mínimo local (e absoluto) em cada ponto crítico.
14.17. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa para traçar gráficos tridimensionais no computador, utilize-o com a janela de inspeção e o po
1. Estude com relação a máximos e mínimos locais a função f x , y = x 3 - 3 x 2 y + 27 y
Utilize um gráfico e/ou curvas de nível para estimar os valores máximos e mínimos locais e pontos de sela da função. Em seguida, use o cálculo para achar esses valores precisamente. f x , y = x y e -