Exercícios Resolvidos de Classificação de Pontos Críticos em Funções de 2 Variáveis
Ver TeoriaEnunciado
Unicamp, Cálculo 2- P2- 2019.1, questão 1
A temperatura de uma placa quadrada de lado centrada na origem (e bordos paralelos aos eixos) é descrita pela função:
- Determine os pontos críticos de e classifique-os.
- Quais as temperaturas máxima e mínima da placa e onde elas ocorrem?
- Escolha um dos pontos críticos e dê a aproximação de no entorno deste ponto, escrevendo seu polinômio de Taylor de segunda ordem (grau 2)
- A partir do ponto em que direções a temperatura aumenta?
Passo 1
Opa! Tudo bem?
Bora ver essa questão aqui!
- Os pontos críticos de são onde as derivadas parciais da função dão zero. Então bora calcular as derivadas parciais:
Queremos então que:
Passo 2
Vamos resolver esse sisteminha. Da primeira equação temos que:
Substituindo na segunda:
E como , temos os pontos críticos:
Passo 3
Para classificar os pontos críticos que achamos, precisamos ver o sinal do Hessiano, que é isso aqui:
Calculando as parciais de segunda ordem:
Testando em cada ponto:
Onde , temos um ponto de sela, então o ponto é um ponto de sela.
Onde e , temos um ponto de máximo, então o ponto é ponto de máximo da função.
Passo 2
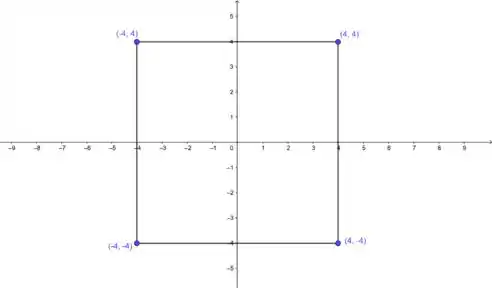
Temos então que verificar a função nessas fronteiras.
Pra primeira fronteira em :
Pra saber os pontos críticos dessa função é só ver onde a derivada zera:
Os pontos críticos aqui então são:
Passo 3
Vamos fazer o mesmo nas outras 3 fronteiras:
Nessa aqui então não temos pontos críticos.
Aqui também não temos pontos críticos.
Então aqui os pontos críticos são:
Passo 6
Vamos testar então o valor da função em todos os pontos que a gente encontrou e nos vértices do quadrado:
Então a temperatura mínima da placa é , e ocorre em e a temperatura máxima é e ocorre em .
Passo 4
Como queremos o polinômio de Taylor de grau 2, vamos precisar das derivadas de primeira e segunda ordem, o que já calculamos lá em cima:
As de segunda ordem:
Passo 5
Agora juntando tudo, nosso polinômio de Taylor de grau 2 ao redor do ponto é:
Que desenvolvendo fica:
Passo 6
Para que a função cresça, precisamos que a derivada direcional seja positiva, então supondo um vetor:
Precisamos que:
Passo 7
Esse vetor tem que ser unitário, então:
Sendo , temos na inequação:
Elevando os dois lados ao quadrado:
Daqui podemos ter:
Ou...
(aqui não há solução)
Então temos que ter:
Passo 8
Vamos ver o intervalo de agora:
Substituindo na inequação:
E aí podemos ter:
Com a outra possibilidade de módulo não vamos ter solução como aconteceu em , então o intervalo de é:
Então, a função cresce nas direções dos vetores do tipo , unitário, sendo que a coordenadas estão no intervalo:
Resposta
- é ponto de sela.
- a temperatura mínima da placa é , e ocorre em e a temperatura máxima é e ocorre em .
- Na direção dos vetores do tipo , unitário, sendo que:
é ponto de máximo.