Seja

E seja definida por

1. Seja o determinante da matriz hessiana de em . Obtenha as funções e tal que
2. Classifique os pontos críticos de em
3. Encontre funções e tal que restrita ao conjunto aberto

Seja estritamente convexa. Desenhe tracejando e explicite

Calculando o determinante:

Assim

Para classificar os pontos críticos de , vamos precisar primeiro encontrar os pontos críticos de , para isso, fazemos

Subtraindo a primeira da segunda:

Resolvendo essa equação do segundo grau, temos que

Ou

Agora, para achar o valor de , vamos substituir essas duas opções de na primeira equação.

Começando por :

Resolvendo essa equação do segundo grau, tiramos que

Ou

Acontece que o nosso ponto crítico deve pertencer ao conjunto , assim, , como é menor que zero, não pertence a .

Então temos um ponto crítico

Agora substituindo , temos

Resolvendo essa equação do segundo grau, chegamos em

Assim, temos mais um ponto crítico:

Agora precisamos classificar essas bagaças.

Sorte que na letra a gente já meio que fez o teste da derivada segunda.

Pra concluir ele, só falta substituir os valores dos pontos críticos e ver o sinal do determinante.

Começando por :

Logo, o ponto é um ponto de sela.

Agora vamos classificar o ponto :

Precisamos então olhar o sinal de :

Assim, o ponto é um ponto de mínimo local de em .

Para ser estritamente convexa a gente precisa que possua apenas pontos de mínimo. E pra garantir isso, a gente precisa que

E que

Para .

Substituindo os valores que a gente já tem, precisamos que

E

Como nosso conjunto é definido por

Temos que

Ainda precisamos esboçar esse negócio.

Pra isso, é só a gente esboçar as retas

E

E nosso conjunto será tudo que tá dentro dessas duas retas, mas sem incluir elas, porque temos o sinal apenas de e não de , sacou?

Assim, vamos desenhar essas retas tracejadas:

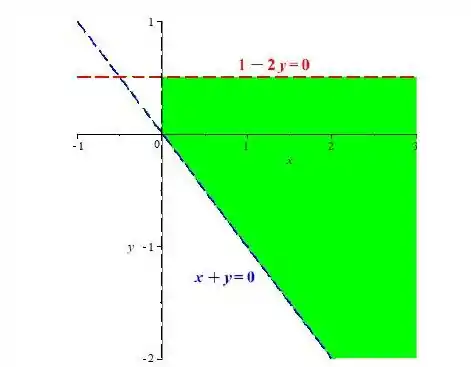
Essa parte verde é a nossa região