Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Classificação de Pontos Críticos em Funções de 2 Variáveis

Ver Teoria
Exercício 721234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071737475767778798081828384858687888990919293949596

Enunciado

UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Profº Otoniel Nogueira - Lista 08, Questão 2

Mostre que a função f ( x ,   y )   =   x   -   1 2   +   y   -   2 2   -   1 admite um mínimo local no ponto P   =   ( 2 ,   1 ) .

Passo 1

Eaee!!! Belezinha? Bom... a questão pede para provarmos que a função f ( x ,   y ) = x - 1 2 + y - 2 2 - 1 admite um mínimo local no ponto P   =   ( 2 ,   1 ) .

Para isso, temos que saber de uma coisinha antes sobre o mínimo local.

Bom... dizemos que a função z = f x , y admite um mínimo local no ponto x 0 , y 0 , se existe um disco aberto R contendo x 0 , y 0 tal que f x , y ≥ f x 0   , y 0 , para todos os pontos x , y em R , conforme ilustra a figura a seguir:

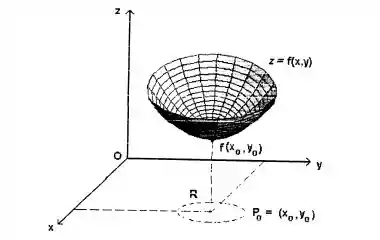
Agora que sabermos dessa definição, vamos provar o que o enunciado nos disse!!

Mas antes, perceba que no ponto P = 2,1 , a função é:

f 2,1 = 2 -   1 2   +   1   -   2 2   -   1 ∴

f 2,1 = 1   +   1   -   1 ∴

f 2,1 = 1  

😉

Passo 2

Então... analisando a nossa função, podemos concluir o seguinte:

x - 1 2 ≥ 0 e y - 2 2 ≥ 0

Dessa forma, se somarmos as duas expressões, obtemos:

x - 1 2 + y - 2 2 ≥ 0

Somando - 1 em ambos os lados, temos:

x - 1 2 + y - 2 2 - 1 ≥ - 1

Note que x - 1 2 + y - 2 2 - 1 éa nossa função f x , y , logo:

f x , y ≥ - 1

Logo, perceba que f 2,1 > - 1 .

Assim, podemos concluir que P   =   ( 2 ,   1 ) é um ponto de mínimo local.

Entendeu direitinho? Responde aee ;)

Resposta

Resposta nos passos

Exercícios de Livros Relacionados

Mostre que f x , y = x 2 + 4 y 2 - 4 x y + 2 em um número infinito de pontos críticos e que D = 0 em cada um. A seguir, mostre que f tem um mínimo local (e absoluto) em cada ponto crítico.
14.17. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa para traçar gráficos tridimensionais no computador, utilize-o com a janela de inspeção e o po
1. Estude com relação a máximos e mínimos locais a função f x , y = x 3 - 3 x 2 y + 27 y
Utilize um gráfico e/ou curvas de nível para estimar os valores máximos e mínimos locais e pontos de sela da função. Em seguida, use o cálculo para achar esses valores precisamente. f x , y = x y e -