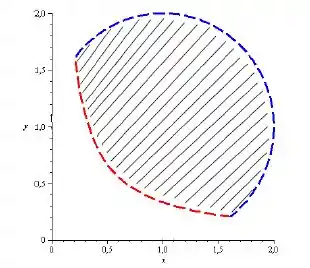
Seja
Seja uma função definida em , onde
Com
- Classifique os pontos críticos de quanto a máximo local, mínimo local ou sela.
- Determine um aberto não vazio do plano (caso exista), tal que restrita à seja estritamente convexa (note que ). Depois desenhe .
Passo 1
Para classificar os pontos críticos, vamos usar o teste da derivada segunda.
Calculando o gradiente:
Passo 2
Encontrando os pontos críticos:
Igualando as coordenadas:
Da primeira equação, temos
Substituindo na segunda equação,
Ou
Assim,
Ou
Temos os pontos
Porém, segundo o enunciado, deve pertencer a . Mas e não pertencem a . De modo que nosso único ponto crítico de em é
Passo 3
Vamos analisar que tipo de ponto crítico é este:
Calculando derivadas segundas:
Calculando essas derivadas no ponto :
Passo 4
Calculando :
Como e , temos que é ponto de mínimo local de em .
Passo 5
Para ser estritamente convexa, isto é para que tenha apenas pontos de mínimo, é preciso que
E que
Para .
Passo 6
É sempre verdadeiro.
Assim
Para .
Dessa forma,
Passo 7
Para esboçar o conjunto , primeiro esboçamos o circulo
E a função
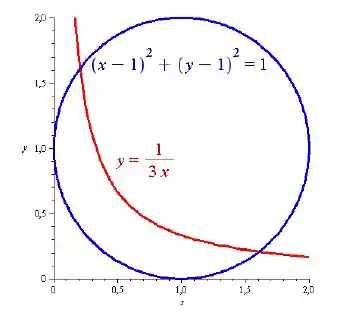
Como nossa região corresponde a área acima de e abaixo de , temos que é
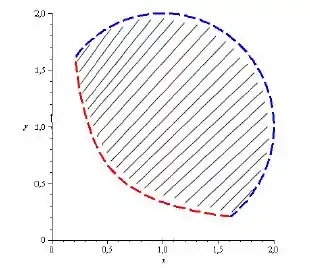
Resposta
- é ponto de mínimo local de em .