1 - Determine e classifique os pontos críticos das funções abaixo relacionadas:
b) ;
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Para essa questão, devemos obter os pontos críticos de e classifica-los como ponto sela ou pontos de máximos ou mínimos locais ou globais.
Mas você sabe o que são pontos críticos?? 🤔
Pontos críticos são os pontos onde suas retas tangentes tem coeficiente angular nulo, ou seja, quando a derivada é igual a .
Para obter os pontos críticos, obtemos o vetor gradiente de , onde
Depois disso, igualamos o gradiente a um vetor nulo e obtemos um sistema em que podemos encontrar os valores para e .
Veja só!
Passo 2
Primeiro vamos obter o gradiente de
Por derivação de polinômios
O segundo termo do gradiente é dado por
Novamente por derivação de polinômios
Com isso, obtemos o gradiente e igualando ao vetor nulo, temos
Assim, obtemos o sistema
A partir desse sistema, podemos tirar conclusão de que e . Ou seja, temos apenas um ponto crítico, no caso
Entendeu?
Passo 3
Para classificar este ponto, devemos obter os valores de , , e e depois substituir os valores de e pelos valores das coordenadas do ponto . Depois disso, devemos calcular o determinante da matriz
Se e , o ponto é classificado como ponto mínimo
Se e , o ponto é classificado como ponto máximo
Já se , o ponto é classificado como ponto sela
Vamos obter derivando com relação a
Vamos obter derivando com relação a
Para obter , derivamos com relação a
Por fim, obtemos derivando com relação a
Tranquilo até aqui?
Passo 4
Por fim, substituímos por e calculamos o determinante
A matriz então fica como
Vemos que e , ou seja, o ponto crítico é um ponto de máximo.
Analisando o gráfico de
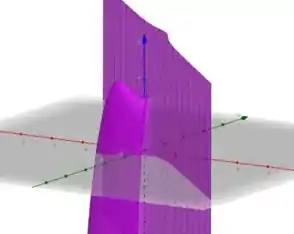
Vemos que o ponto é um ponto de máximo local, já que existem valores maiores na imagem de .
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta
máximo local.