Exercícios Resolvidos de Classificação de Pontos Críticos em Funções de 2 Variáveis
Ver TeoriaEnunciado
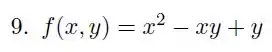
Passo 1
Assim que a gente vir essas palavrinhas mágicas, “classifique os pontos críticos”, o nosso reflexo tem que ser: calcular as derivadas parciais, igualá-las a 0 e depois mandar ver no teste da derivada segunda! Então vamos fazer isso, começando pelas derivadas parciais!
Passo 2
Show! Agora vamos igualar essas derivadas a 0:
Da segunda equação, tiramos
Substituindo na primeira, vai dar:
Beleza, então só tem um ponto crítico, o ponto .
Passo 3
Agora só resta classificar esse ponto crítico, usando o teste da derivada segunda, então vamos calcular as derivadas segundas! Lembrando que e . Assim,
Também temos:
E pras derivadas mistas:
Passo 4
Pronto! Agora podemos aplicar o teste da derivada segunda :) O nosso determinante vai ser:
Assim, como , o ponto é um ponto de sela.
Resposta
Exercícios de Livros Relacionados
Mostre que f x , y = x 2 + 4 y 2 - 4 x y + 2 em um número infinito de pontos críticos e que D = 0 em cada um. A seguir, mostre que f tem um mínimo local (e absoluto) em cada ponto crítico.
14.17. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa para traçar gráficos tridimensionais no computador, utilize-o com a janela de inspeção e o po
1. Estude com relação a máximos e mínimos locais a função f x , y = x 3 - 3 x 2 y + 27 y
Utilize um gráfico e/ou curvas de nível para estimar os valores máximos e mínimos locais e pontos de sela da função. Em seguida, use o cálculo para achar esses valores precisamente. f x , y = x y e -