Exercícios Resolvidos de Classificação de Pontos Críticos em Funções de 2 Variáveis
Ver TeoriaEnunciado
UNICAMP. Calculo 2. 2021.2 - 6ª Manhã. Prova: P1. Questão 1.
Encontre e classifique todos os pontos críticos da função.
estabelecendo se são pontos de sela, pontos de mínimo local ou absoluto, pontos de máximo local ou absoluto. Justifique todos os detalhes!
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão, foi dada uma função e foi pedido para que calculássemos os pontos críticos dessa função e também temos que classificar esses pontos como sendo pontos de sela, máximos ou mínimos locais ou absolutos.
Entendeu? Então como podemos fazer isso?? 🤔🤔
Os pontos críticos de uma função, são obtidos derivando em relação a e depois a e igualando a . A combinação dos valores que vamos obter para a solução dessas derivadas, vão ser os pontos críticos de .
A partir daí temos que analisar se esses pontos críticos são pontos de sela, de máximos ou de mínimos e para isso, temos que fazer algumas analises a mais.
Mas calma aí! Vamos por partes!
Bora encontrar os pontos críticos!
Passo 2
Primeiramente, vamos derivar com relação a
Quando derivamos com relação a , a variável se comporta como uma constante e sabemos que a derivada de uma constante é igual a .
Pelo método de derivação polinomial, temos
Agora faremos o mesmo para obter a derivada de com relação a
Agora é a vez do se comportar como uma constante.
Pelo método de derivação polinomial, temos
Igualando e a , vamos obter um sistema de equações
Organizando um pouquinho mais
Tranquilo até aqui? 👀
Passo 3
Se a gente isolar na primeira equação, vamos obter
Substituindo na segunda equação, tiramos que
Organizando um pouquinho, chegamos em
Vamos calcular as raízes dessa equação por Bhaskara.
Substituindo na primeira equação, temos
Com isso, obtemos nosso primeiro ponto
Agora substituindo na primeira equação, temos
Assim, obtemos outro ponto
Esses dois pontos que acabamos de encontrar, são os pontos críticos que vamos chamar de e .
Está acompanhando? 😁
Passo 4
Agora, queremos saber se os pontos que encontramos são pontos de máximo, de mínimo ou ponto de sela.
Pra isso, temos que calcular as segundas derivadas de derivando e com relação a e .
Calculando , temos
Pelo método de derivação polinomial
Para
Pelo mesmo método de derivação
Agora vamos obter
Novamente pelo mesmo método de derivação
E por último, vamos obter
Montando uma matriz determinante com esses termos que acabamos de obter
Bacana, não é?
Passo 5
Vamos usar para definir se e são pontos máximos ou pontos mínimos.
Substituindo as coordenadas dos pontos em e encontrarmos que e o ponto é classificado como ponto de mínimo.
Já de após as substituições e , o ponto é classificado como máximo.
Mas se , o ponto é classificado como ponto sela.
Primeiro vamos analisar o ponto
, logo o ponto é classificado como um ponto sela!
Agora vamos analisar o ponto
e , logo, o ponto é classificado como um ponto máximo!
Mas será que é um ponto máximo local ou é um máximo global? 🤔
Pra responder essa pergunta, vamos analisar a imagem de .
Por ser uma função polinomial, a imagem de é definida de a . Se calculássemos o valor de no ponto , vamos obter
Existem pontos em em que a imagem é maior que , logo é um ponto de máximo local.
Vamos dar uma olhada no gráfico de pra exemplificar o que acabamos de calcular?
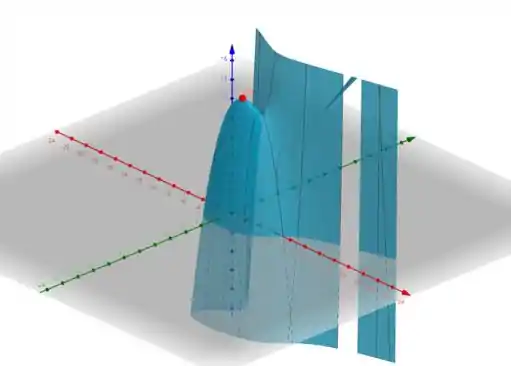
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
ponto sela
ponto de máximo