Exercícios Resolvidos de Classificação de Pontos Críticos em Funções de 2 Variáveis
Ver TeoriaEnunciado
Encontre os pontos e os valores mínimos e máximos locais e os pontos de sela (se houver) da função
Esboce o gráfico da função em torno dos pontos encontrados acima.
Observação: não é preciso esboçar o gráfico de toda função; apenas mostre como é o gráfico perto dos pontos de mínimo local, máximo local ou pontos de sela determinados.
Passo 1
O que o enunciado está pedindo é para gente classificar os pontos críticos dessa função. Para ser ponto crítico, precisa zerar as derivadas ao mesmo tempo:
Vamos encontrar para que pontos isso acontece. Calculando as derivadas:
Descobrindo onde elas zeram ao mesmo tempo:
Aí a gente fica com esse sisteminha para resolver:
Passo 2
Da primeira equação, a gente pode escrever
Daí a gente tem que ou . Vamos olhar cada caso
-
Substituindo na segunda equação
Daí a gente tem dois pontos:
-
Substituindo na segunda equação
Daí a gente tem dois novos pontos:
Aí achamos quadro pontos críticos:
Passo 3
Para classificar esses pontos, a gente precisa calcular o determinante 𝐻(𝑃0):
Se ele for positivo, nosso ponto é de máximo ou de mínimo. Aí se for de mínimo e se for de máximo . Maaas se for negativo, nosso ponto é ponto de sela. (Se for não se sabe).
Vamos calcular então essas derivadas de segunda ordem:
Passo 4
Agora é calcular esse determinante para os nossos pontinhos! Vamos calcular :
Como , e esse é um ponto de máximo.
Vamos calcular :
Como , esse é um ponto de máximo ou mínimo. E como , sabemos que esse ponto é de mínimo.
Vamos calcular :
Como , esse é um ponto de sela.
Vamos calcular :
Como , esse é um ponto de sela também.
Passo 5
Vamos agora descobrir o valor da função nesses pontos e esboçar o gráfico da função pertinho deles.
- , ponto de máximo. Ao redor dele, a função parece um paraboloide elíptico virado para baixo.
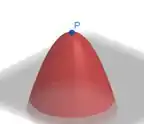
E vale
- , ponto de mínimo. Ao redor dele, a função parece um paraboloide elíptico virado para cima.
E vale
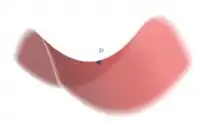
- , ponto de sela. Ao redor dele, a função parece uma sela de cavalo como o nome já diz haha.
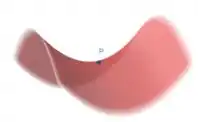
E vale
- , ponto de sela também. Vai ter a mesma carinha do ponto anterior. E vale
Ufa! Acabamos!
Resposta
, ponto de máximo. Ao redor dele, a função parece um paraboloide elíptico virado para baixo e nele ela vale .
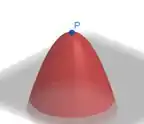
, ponto de mínimo. Ao redor dele, a função parece um paraboloide elíptico virado para cima e nele ela vale .
, pontos de sela. Ao redor deles, a função parece uma sela de cavalo como o nome já diz. E neles, ela vale .
