Exercícios Resolvidos de Classificação de Pontos Críticos em Funções de 2 Variáveis
Ver TeoriaEnunciado
UFABC. Cálculo. Funções de Várias Variáveis. Lista 5 - Pontos Críticos, Máximos e Mínimos, Multiplicadores de Lagrange. Questão 1a.
1 - Determine e classifique os pontos críticos das funções abaixo relacionadas:
a) ;
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Essa questão nem nos deu “bom dia” e já mandou a gente determinar os pontos críticos e classifica-los como máximos ou mínimos.
A função que vamos usar será o polinômio
Ta lembrado de como calculamos os pontos críticos de uma função??
Os pontos críticos de uma função são obtidos calculando o vetor gradiente de e igualando a um vetor nulo, por exemplo
Com isso, vamos obter um sistema.
A partir daí a gente calcula os possíveis valores que satisfazem esse sistema. Esses valores são as coordenadas dos nossos pontos críticos.
Entendi, mas e como classificamos um ponto crítico??
Para classificar um ponto crítico devemos montar uma matriz formada pelas derivadas parciais , , e , dessa forma
Substituímos os pontos que encontramos nas derivadas.
Calculando esse determinante, ou simplesmente , se for maior que e também for maior que , o ponto é classificado como ponto de mínimo local.
Se for maior que e for menor que , o ponto é classificado como ponto de máximo local.
Já se , o ponto não é máximo nem mínimo.
Entendeu? Podemos ir para os cálculos agora.
Passo 2
Vamos calcular o vetor gradiente de , primeiro vamos calcular . Nesse momento se comporta como uma constante.
Por derivação de polinômios, temos
Agora vamos calcular . É a vez de se comportar como constante.
Por derivação de polinômios, vemos que
Com esses resultados, nosso vetor gradiente é dado como
Igualando a um vetor nulo, temos
Obtemos o sistema
Isolando e em um lado da igualdade, temos
Com isso, encontramos apenas um ponto crítico dado por .
Tranquilo até aqui?
Passo 3
O próximo passo é classificar o ponto que encontramos, pra isso vamos calcular as derivadas que vimos no início.
Vamos calcular derivando com relação a .
Vamos obter derivando com relação a .
Vamos obter derivando com relação a .
Por fim, obtemos derivando com relação a .
Vamos montar a matriz e calcular o determinante.
Obtemos , e observando , vemos que ele também é maior que , logo o ponto é um ponto de mínimo.
Para sabermos se é mínimo global ou local, temos que analisar a função ou seu gráfico. Vemos que tanto em quanto em a ordem polinomial é 2, ou seja, eles têm a cara do gráfico de , ou seja
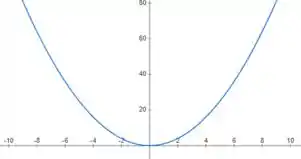
Logo, podemos afirmar que o ponto é um ponto de mínimo global.
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
, mínimo global.