Exercícios Resolvidos de Classificação de Pontos Críticos em Funções de 2 Variáveis
Ver TeoriaEnunciado
UFABC. Cálculo. Funções de Várias Variáveis. Lista 5 - Pontos Críticos, Máximos e Mínimos, Multiplicadores de Lagrange. Questão 2b.
2 - Encontre o máximo e mínimo globais de cada uma das seguintes funções:
b) , na região triangular com vértices , e ;
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão, vamos calcular o ponto máximo e o ponto mínimo que a função assume dentro da área limitada pelo triângulo de vértices , e .
Ok! Sabemos calcular os pontos de máximos e mínimos de uma função em toda sua imagem, mas como fazemos isso em uma área limitada??
Relaxa! Vamos usar o que já sabemos para encontrar os pontos críticos de , mas vamos ignorar os pontos que não estão dentro da área do triangulo.
O que vai mudar é de devemos aplicar uma análise nas bordas da área do triângulo, encontrando os pontos onde a função assume os maiores e os menores valores.
Depois disso, vamos comparar os resultados e definir os extremos de que obtemos.
Veja só!
Passo 2
Vamos começar pelo método comum. Vamos derivar com relação a e e igualar a para obter um sistema.
Por derivada de polinômios
Vamos obter a outra derivada
Também por derivada de polinômios
Assim, igualando as duas equações a , obtemos o sistema
Manipulando essas equações, podemos chegar a
Com isso vemos que .
Os únicos valores que podemos definir para , é e .
Ou seja, temos dois pontos para ficarmos de olho e .
Porém, vamos ver que o ponto está fora da nossa área do triangulo, então ele não nos interessa. Então temos apenas !
Tranquilo?
Passo 3
Vamos analisar a área do triângulo.
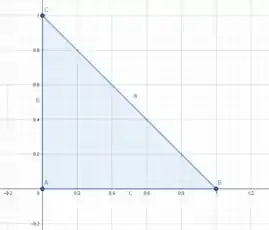
Temos que definir as equações que delimitam nosso espaço.
Para a reta que passa por , vemos que é .
Para a reta , vemos que é .
Já para a reta podemos definir pela matriz
Ou simplesmente por
Vamos analisar o comportamento da função quando estamos no limite do triangulo.
Quando estamos na borda , temos
Imaginando o gráfico de podemos dizer que no intervalo de , só aumenta, então o ponto é o valor mínimo e o ponto é o valor máximo dessa borda.
Como já suspeitávamos do ponto , não vamos adicioná-lo novamente. Mas vamos adicionar o ponto à nossa lista.
Entendeu?
Passo 4
Analisando a borda , temos
Temos exatamente o mesmo gráfico que acabamos de ver, apenas em outro eixo.
Podemos copiar os valores de antes apenas trocando os eixos de e .
Com isso, acrescentamos o ponto à nossa listinha.
Agora, analisando a borda , temos
Organizando um pouquinho mais essa função, temos
Com isso, vamos calcular os pontos críticos dessa função pelo método comum.
Substituindo esse resultado na equação , temos
Portanto, encontramos o ponto .
Está acompanhando?
Passo 5
Por fim, vamos obter os valores e para cada ponto e escolher o maior e o menor valor como máximo e mínimo.
Para o ponto
Para o ponto
Para o ponto
Por fim, para o ponto
Comparando os resultados, vemos que em e em a função atingiu o maior valor, portanto, esses pontos são nossos pontos de máximos globais.
Já o menor valor foi obtido no ponto , então este ponto é o nosso mínimo global.
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
e : Máximos globais.
: Mínimo global.